MarkFL
Gold Member
MHB
- 13,284
- 12
Here is the question:
I have posted a link there to this thread so the OP can view my work.
Calculus volume help please?
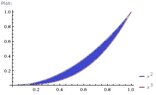
Let T be the region enclosed between the graphs of y=x^2 and y=x^3
A. Use the washer method to find the volume of the solid of revolution formed when T is revolved about the Y-axis.
B. Use the shell method to compute the volume of the solid of revolution described in Part A.
I have posted a link there to this thread so the OP can view my work.