spizma
- 34
- 0
Homework Statement
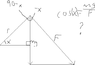
A small particle of mass m is pulled to the top of a frictionless
half-cylinder (of radius r) by a cord that passes
over the top of the cylinder, as illustrated in Figure
P7.20. (a) If the particle moves at a constant speed, show
that F = mg*cos(x). (Note: If the particle moves at constant
speed, the component of its acceleration tangent to the
cylinder must be zero at all times.)
See picture 1
Homework Equations
Force of gravity = mg
cos(x)=adj/hyp
The Attempt at a Solution
Well I figured that what you really need to do is find an equation giving the force vector of the particle. Picture 2 illustrates what I figured. The smaller triangle is the one from the half circle. The larger triangle is for the force vector of the triangle. Because the force vector is tangent to the circle, the radius must be perpendicular with the force vector. From there you can find the top angle of the large triangle. From that you can write cos(x)= mg/F. That gives you F = mg/cos(x), which is wrong. This has been bothering me for a while. The solution is probably something very simple I'm just missing. Could someone please help?