Mathematica newby needs help with plot

[yougene]

I picked up Mathematica 6.0 a couple days ago, so bear with me please.

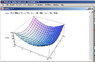
1) Plot3D[{x^2 + y^2}, {x, -10, 10}, {y, -10, 10}]
returns a blank graph whereas when I set the boundaries from 0 to 2 it returns the actual graph! Why isn't it working?2) When typing equation f into the Plot3D function( e.g {x^2 + y^2} ), is it implied that x^2 + y^2 == z ? I would think so, but using == doesn't work in the Plot3D expression.

 

[Dale]

Plot3D[{x^2 + y^2}, {x, -10, 10}, {y, -10, 10}] returns the correct plot for me with no problem.

Yes, that is the implication for Plot3D, however it is not expressed as an equation since you cannot use Plot3D to plot e.g. a sphere using an equation like x^2 + y^2 + z^2 == 1. Instead, the first argument to Plot3D must be a function of the variables in the second and third arguments. This is also done for syntactical consistency with other plotting routines where a 3rd coordinate wouldn't make as much sense (e.g. density plots and contour plots)

 

[yougene]

Plot3D[{x^2 + y^2}, {x, -10, 10}, {y, -10, 10}] returns the correct plot for me with no problem.

Hmmm, perhaps my copy is broken.

Yes, that is the implication for Plot3D, however it is not expressed as an equation since you cannot use Plot3D to plot e.g. a sphere using an equation like x^2 + y^2 + z^2 == 1. Instead, the first argument to Plot3D must be a function of the variables in the second and third arguments. This is also done for syntactical consistency with other plotting routines where a 3rd coordinate wouldn't make as much sense (e.g. density plots and contour plots)

Would there be a simple way to plot an implicit function?

 

[CompuChip]

You can rewrite the function in the form z = f(x, y) and use Plot3D:

Solve[z^2 + x^2 + y^2 == R^2, z] /. R -> 1
Plot3D[z /. %, {x, -1, 1}, {y, -1, 1}, BoxRatios -> {1, 1, 1}]

or parametrize it:

ParametricPlot3D[{r Cos[theta] Sin[phi], r Sin[theta] Sin[phi], r Cos[phi]} /. r -> 1, {phi, 0, \[Pi]}, {theta, 0, 2 \[Pi]}]

or you may use RegionPlot3D:

RegionPlot3D[x^2 + y^2 + z^2 <= 1, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}]

 

[yougene]

Ahh, those worked.

What does /. R -> 1 do precisely?

From what I'm gather /. means a rule is to follow. lhs -> rhs represents "a rule that transforms lhs to rhs."

So is /. R -> 1 the equavalent of saying R = 1 or R approaches 1?

 

[Dale]

Ahh, those worked.

What does /. R -> 1 do precisely?

From what I'm gather /. means a rule is to follow. lhs -> rhs represents "a rule that transforms lhs to rhs."

So is /. R -> 1 the equavalent of saying R = 1 or R approaches 1?

It is the equivalent of temporarily saying R = 1. In other words, if you do set R = 1 then it applies to all expressions using R, but by using a rule you apply it only for that expression.

 

[yougene]

So it's like setting a local variable. How does it contrast with Mathematica's ability to set local variables within lists. e.g. {x = 1, expr}Thanks for the help guys.

 

[CompuChip]

It doesn't contrast with it. If you do
{X = 1, expr}
then it will return a list
{1, expr}
and in addition will assign the value 1 to X anywhere you use it. If somewhere else you wrote
Solve[X^2 == 4, X]
and execute it after the above statement, you will get errors because it cannot evaluate
Solve[1^2 == 4, 1]

IMO and experience assigning variables globally should always be avoided unless you have really really really good reasons to do it (and I mean: really very good reasons). There are sufficiently good constructs not to have to do it, like replacements, as in
x^2 + y^2 == f[r] /. {x -> r Cos[theta], y -> r Sin[theta], f[t_] :> t^2}
and temporary assignments as in
Block[{i = 3, x = 4}, DoSomethingWith[i, x];]
Module[{i = 3, x = 4}, DoSomethingWith[i, x];]
You can even assign replacement lists to variables, as in:
repl = {x -> ..., y -> ..., z :> ..., q'[0] -> ...}
and use them everywhere
x^2 - z y / q'[0] /. repl
(So, I admit, this is an exception to the rule about assigning variables --- but it's about the only one).

I hardly ever find myself assigning variables (and if I do for a quick test, I always quit the kernel afterwards). It prevents a lot of unexpected results.

 

[Dale]

I agree with CompuChip. The only time I use expressions like x=1 is when I know I am not going to save it or use it some other time.

 

[EnumaElish]

Ahh, those worked.

What does /. R -> 1 do precisely?

From what I'm gather /. means a rule is to follow. lhs -> rhs represents "a rule that transforms lhs to rhs."

So is /. R -> 1 the equavalent of saying R = 1 or R approaches 1?

/. can be thought of as a conditioning operator similar to writing $$\left.\frac {\partial y}{\partial x}\right|_{x=0}$$

In Mathematica, that last expression would be ($\partial_x$ y)/.x->0

/.R -> 1 is a local literal replacement rule. Although it is mostly used to assign temp values, it can be used to replace any literal part of the preceding expression with anything else. For example,

(x+y)^2 - z^2/.(x+y)^2 -> r^4 yields r^4 - z^2.

But (x^2 + y^2 + 2 x y) - z^2 /. (x + y)^2 -> r^4 returns x^2 + 2 x y + y^2 - z^2. The replacement has no effect when it isn't literal.