Mathmatic relationship (Linear,Quadratic,Exponential)

[Ltpenguin]

Homework Statement

State the mathematical relationship (Linear,Quadratic,Exponential) and determine the regression equation for this relationship.

Homework Equations

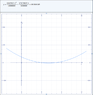
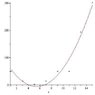
X| 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 |
Y| 50 | 14 | 2 | 14 | 50| 50 |194|302|

The Attempt at a Solution

?.? i input the information into my TI-83 Plus and i get an error when trying to make a regression equation and i cannot figure out the type of relationship it is(linear,quadratic, or exponential)

anyone know how to do a table? i did the difference thing.

 

[adjacent]

State the mathematical relationship (Linear,Quadratic,Exponential) and determine the regression equation for this relationship.

Look carefully at the graph.
How does a quadratic graph normally look like?
How does an exponential graph normally look like?
And how does a linear graph normally look like?
If you know all these, then you can answer your question.

 

[Ltpenguin]

Look carefully at the graph.
How does a quadratic graph normally look like?
How does an exponential graph normally look like?
And how does a linear graph normally look like?
If you know all these, then you can answer your question.

It would appear to be a quadratic but when i try to make the formula on my TI-83 it doesn't make the equation it gives and error.

 

[adjacent]

It would appear to be a quadratic but when i try to make the formula on my TI-83 it doesn't make the equation it gives and error.

The $y$ value for $x=11$ seems to be giving the error. Try removing that.
Obviously this is not a linear graph -Linear graphs should be a straight line.
This is also not a exponential graph. Do you know why?

 

[Ltpenguin]

The $y$ value for $x=11$ seems to be giving the error. Try removing that.
Obviously this is not a linear graph -Linear graphs should be a straight line.
This is also not a exponential graph. Do you know why?

It is a Quadratic because it forms a parabola and not an exponential graph because an exponential graph would not lower at any point it would continune to go on a sharp incline. Also i still got an error when i removed x=11 / y=50

Got another calculator my seems to malfunction when doing the calc. y=ax^2+bx+c A=3.267857 B= -35.357214 c=89.589285

 

[adjacent]

Got another calculator my seems to malfunction when doing the calc. y=ax^2+bx+c A=3.267857 B= -35.357214 c=89.589285

Then your calculator is broken(Or reached some limit?)
My calculator does that without malfunctioning. See:

 

[SammyS]

...

Got another calculator my seems to malfunction when doing the calc. y=ax^2+bx+c A=3.267857 B= -35.357214 c=89.589285

That agrees with adjacent's recent posted value.

If you discard the point with x = 11, the rest of the points lie exactly on a parabola. For this parabola, A, B, and C are all integers.

 

[thelema418]

If there is a context to the problem, you may want to consider that. Sometimes output variables are non-negative. Examples would be height, age, test grades. If that is a constraint on this data set, it may be better to drop the point (11, 50) before running the regression.

 

[LCKurtz]

Just for confirmation, using all the given points, Maple gives exact fractions:$$
a=\frac {183}{56},~b=-\frac{495}{14},~c=\frac{5013}{56}$$which agrees with the other solutions given as decimals.

 

[adjacent]

Just for confirmation, using all the given points, Maple gives exact fractions:$$
a=\frac {183}{56},~b=-\frac{495}{14},~c=\frac{5013}{56}$$which agrees with the other solutions given as decimals.

Isn't that the parabola of best fit including that $x=11$ point?
None of the points in the table lies in that(Your) parabola

 

[LCKurtz]

Just for confirmation, using all the given points, Maple gives exact fractions:$$
a=\frac {183}{56},~b=-\frac{495}{14},~c=\frac{5013}{56}$$which agrees with the other solutions given as decimals.

Isn't that the parabola of best fit including that $x=11$ point?

Isn't that what I said above?

None of the points in the table lies in that(Your) parabola

You wouldn't expect them to be exactly on the best least squares fit.

 

[Ray Vickson]

Isn't that what I said above?



You wouldn't expect them to be exactly on the best least squares fit.

When I do it in Maple I get $a = 183/56, b = -495/15, c = 5017/56$, so my $c$ is a bit different from what you wrote.

If, instead of a least-squares solution we minimize the absolute error solution
$$\sum_{i=1}^8 |Y_i - a - b X_i - c X_i^2|$$
we obtain $a = 77, b = -30,\, c = 3$. The errors are all zero except at the point x = 11, where the absolute error is 60. Basically, the mean absolute-deviation method automatically de-emphasizes the point x = 11 and gives an exact fit to the rest of the data.

For the benefit of the OP: the least-absolute solution can be obtained by solving a so-called linear programming problem:
$$\text{minimize } \sum_{i=1}^8 z_i\\ \text{subject to the constraints}\\ z_i \geq Y_i - a - b X_i - c X_i^2, \: i=1, \ldots, 8\\ z_i \geq a + b X_i + cX_i^2 - Y_i, \: i = 1, \ldots, 8$$
Here, the variables are $a,b,c, z_1, z_2, \ldots, z_8$. Such problems can be solved using the EXCEL Solver tool, or using the (free) trial version of LINGO (from LINDO Systems, Inc.) plus numerous free "linear programming solution" tools available from the web.

 

[LCKurtz]

When I do it in Maple I get $a = 183/56, b = -495/15, c = 5017/56$, so my $c$ is a bit different from what you wrote.

I just ran it again. Apparently I mistyped the numerator for $c$ because I do get $5017/56$ as you do. But for $b$ I still get $-495/14$.

 

[Ray Vickson]

I just ran it again. Apparently I mistyped the numerator for $c$ because I do get $5017/56$ as you do. But for $b$ I still get $-495/14$.

I mis-typed $b$; it should have been as you state.