Matrix Elements via Feynman Diagrams

[Sum Guy]

Hello everyone,

I am currently trying to understand how we can use feynman diagrams to estimate the matrix element of a process to be used in fermi's golden rule so that we can estimate decay rates. I am trying to learn by going through solved examples, but I am struggling to follow the logic of the solutions provided.

For instance consider the question;

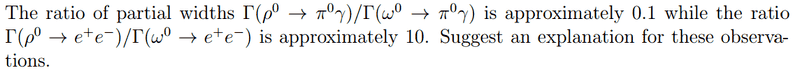
The feynman diagram for one possible method of decay is shown for the rho 0 meson:

And the following solution is provided:

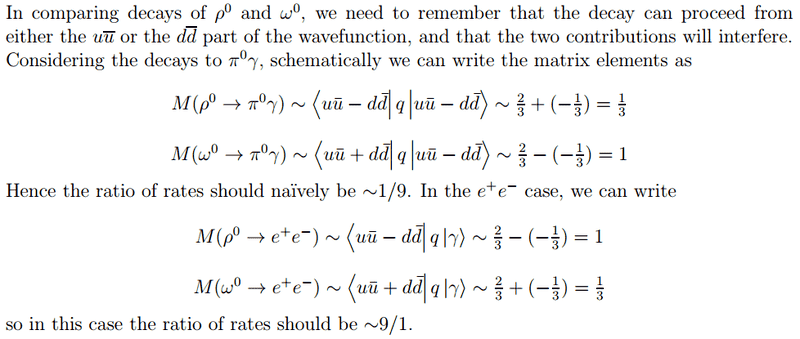
I have a few questions arising from this solution. We are told to consider that the decay can proceed from either the uubar or ddbar part of the wavefunction, but should we not also consider that the photon vertex can sit on u or ubar (and hence introduce a factor of 2 to the matrix element - I know this is not important when considering ratios, but is this still correct?)

Why is the strength of the interaction and the vertex factor given by (-1/3) in the case of d quarks, not (+1/3)? In general I thought that when considering vertex factors we should take the magnitude of the charge of the particle involved, otherwise could we not have a factor of (-1/3) from the photon emitted from the down quark and a factor of (+1/3) from the photon emitted from the anti down quark, which would then cancel?

If we are trying to estimate the rate of decay of a given process, and that process can occur by multiple methods, why do they then have a cancelling out effect? Surely these should all contribute to the rate of decay! e.g. should the first matrix element not be ~ 2/3 + 1/3?

Why can we ignore the cross terms <uubar|q|ddbar>?

Thank you.

 

[mfb]

Why is the strength of the interaction and the vertex factor given by (-1/3) in the case of d quarks, not (+1/3)? In general I thought that when considering vertex factors we should take the magnitude of the charge of the particle involved, otherwise could we not have a factor of (-1/3) from the photon emitted from the down quark and a factor of (+1/3) from the photon emitted from the anti down quark, which would then cancel?

You add complex amplitudes if multiple processes lead to the same final state. For the $\rho$ decay to pion plus photon, both processes (decay as uu and decay as dd) have the same complex phase and add up, for the $\omega$ decay they have opposite sign and subtract. For the decay "to a photon" (to ee), you have the opposite case.

You can only add magnitudes of (squared) amplitudes if the processes lead to different final states.