MarkFL
Gold Member
MHB
- 13,284
- 12
Here is the question:
I have posted a link there to this topic so the OP can see my work.
What are the critical values of this function?
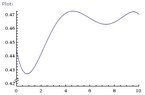
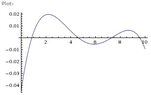
A model for the average price of a pound of white sugar in a certain country from August 1993 to August 2003 is given by the function
S(t) = −0.00003237t^5 + 0.0009037t^4 − 0.008956t^3 + 0.03629t^2 − 0.04467t + 0.4438
where t is measured in years since August of 1993. Estimate the times when sugar was cheapest and most expensive during the period 1993-2003. (Round your answers to three decimal places.)
I have posted a link there to this topic so the OP can see my work.