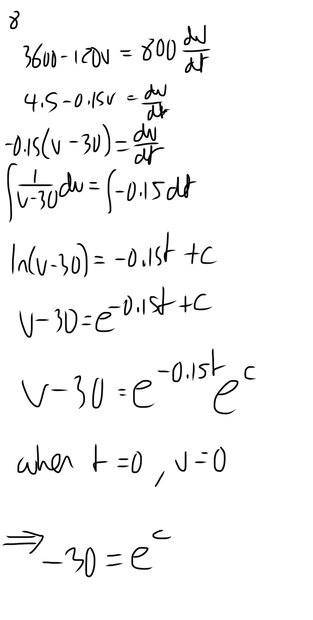Homework Help Overview
The discussion revolves around a physics problem involving a car with a mass of 800 kg and a driving force of 3600 N, which experiences resistive forces. Participants are tasked with formulating an equation to demonstrate that the maximum speed is 30 m/s, assuming the driving force remains constant.
Discussion Character
Approaches and Questions Raised
- Participants explore the formulation of differential equations related to the motion of the car, questioning the behavior of integrands and the implications of initial conditions. Some suggest using integrating factors, while others discuss the physical interpretations of mathematical results.
Discussion Status
The discussion is active, with various interpretations and approaches being explored. Some participants have offered guidance on the mathematical setup, while others have raised questions about the validity of certain integrals and their physical implications. There is no explicit consensus on the best approach yet.
Contextual Notes
Participants are navigating constraints related to the assumptions of the problem, such as the behavior of the driving force and resistive forces, as well as the implications of initial conditions on the equations derived.