- #1
csc2iffy
- 76
- 0
Homework Statement
We have to solve this problem using only what we learned in calculus (no linear programming)
I attached a picture to help :)
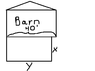
A farmer wants to build a rectangular pen. He has a barn wall 40 feet long, some or all of which must be used for all or part of one side of the pen. In other words, with f feet of of fencing material, he can build a pen with a perimeter of up to f+40 feet, and remember he isn't required to use all 40 feet.
What is the maximum possible area for the pen if 100 feet of fencing is available?The attempt at a solution
I attempted to solve by finding the critical points of the derivative:
2x+y=100 --> y=100-2x
x(100-2x)=100x-2x^2
f'(x)=100-4x
100-4x=0 --> x=25
2(25)+y=100 --> y=50
A=1250
BUT I realize this is wrong because if y=50, then the side of the barn needs an extra 10 feet, but all of the fencing material has been used by the other 3 sides. Help please?
We have to solve this problem using only what we learned in calculus (no linear programming)
I attached a picture to help :)
A farmer wants to build a rectangular pen. He has a barn wall 40 feet long, some or all of which must be used for all or part of one side of the pen. In other words, with f feet of of fencing material, he can build a pen with a perimeter of up to f+40 feet, and remember he isn't required to use all 40 feet.
What is the maximum possible area for the pen if 100 feet of fencing is available?The attempt at a solution
I attempted to solve by finding the critical points of the derivative:
2x+y=100 --> y=100-2x
x(100-2x)=100x-2x^2
f'(x)=100-4x
100-4x=0 --> x=25
2(25)+y=100 --> y=50
A=1250
BUT I realize this is wrong because if y=50, then the side of the barn needs an extra 10 feet, but all of the fencing material has been used by the other 3 sides. Help please?
Attachments
Last edited: