B Maximizing Mechanical Advantage in Levers: Investigating Size and Shape

[Joorge]

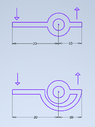
I have these 2 levers seen from above, that is, gravity does not affect.
In the first one, it is clear to me that it is a first class lever and that the mechanical advantage is 2x.
What about the second one? Does it make any difference?
I'm wondering if I need to 'cross' the fulcrum (so to speak) or not to get mechanical advantage.

 

[Lnewqban]

Welcome!
What do you mean by "to cross the fulcrum"?
Is this homework?

 

[Gordianus]

What "law" do you use to analyze levers?

 

[Joorge]

Welcome!
What do you mean by "to cross the fulcrum"?
Is this homework?

Well, I'm 60 years old... I don't think so. I mean if I need to touch (so to speak) the center. Sorry about my ignorance and my English.

 

[Joorge]

What "law" do you use to analyze levers?

The only thing I learned long time ago was distance_A x Force_A = distance_B x Force_B.
What is intriguing to me if is passing through the center (so to speak) is needed. Sorry about my English.

 

[hmmm27]

What if the lever was filled in ? on the right hand side where the gap is ? What if there were holes drilled into it ? in random places.

 

[Joorge]

If you want to fill in the right hand is up to you, but that's not my question.
You can make some holes too or paint the whole thing in pink.
Did you get your gold member answering like that?

 

[hmmm27]

No, I got the gold membership for the royalties and timeshare on the company jet.

My question was, does it make a difference if it's painted pink ? or a piece of string or welded wire bridged the beginning of the gap on the left side.

 

[Joorge]

My question is if the second one could be consider a lever provided that is crossing the fulcrum by outside and if so, if the mechanical advantage would be the same in both cases, or more, or less.

I don't know it because I have very basic understanding of Physics, that's the reason I came here. If you want to laugh at me is ok, I have no trouble with my ego, but I'd prefer to get some kind of coherent answer. Thanx :)

 

[hmmm27]

Not laughing at you.

If you push the leftmost point of the lever down 2cm, how much does the rightmost point push up ? Is it the same, or different from the original lever.

 

[Lnewqban]

Well, I'm 60 years old... I don't think so. I mean if I need to touch (so to speak) the center. Sorry about my ignorance and my English.

The force that you apply will reach that other end via the fulcrum, no matter what trajectory it follows.

Yes, the mechanical advantage will still be 2.
The force that the fulcrum will “feel” will be the same as well.

Perhaps you will feel the lever more springy, due to the additional deflection of the longer trajectory.
I don’t know enough English to see what is wrong with yours.

 

[jbriggs444]

Yes, the mechanical advantage will still be 2.

To expand a bit on this

It is still a rigid object. It still has three points where forces are applied. The positions of those points relative to one another has not changed. Everything else is just pink paint.

 

[Lnewqban]

Please, see:
http://www.tpub.com/machines/1c.htm

 

[Joorge]

Not laughing at you.

If you push the leftmost point of the lever down 2cm, how much does the rightmost point push up ? Is it the same, or different from the original lever.

I have no idea. That's the reason I'm asking. Thanks anyway.

 

[Joorge]

The force that you apply will reach that other end via the fulcrum, no matter what trajectory it follows.

Yes, the mechanical advantage will still be 2.
The force that the fulcrum will “feel” will be the same as well.

Perhaps you will feel the lever more springy, due to the additional deflection of the longer trajectory.
I don’t know enough English to see what is wrong with yours.

Thank you :)

 

[jbriggs444]

I have no idea. That's the reason I'm asking. Thanks anyway.

The attempt was to get you to think of the lever as a rigid body.

No matter how many spurs you hang on it or how serpentine you make it or how many holes you drill into it, it is still a rigid structure. All the points on a rigid body move together with each other.

A rigid body can rotate. Or it can move around from place to place (translate). But it cannot bend, twist, squish, stretch or flow.

With this in mind, if you hold the pivot point fixed and push the left end (the long side) down by two cm, how far must the right end move and in which direction?

 

[Lnewqban]

Thank you :)

You are welcome, Joorge.

You can also use the concept of work in = work out, considering work as force x length of arc described by that force.
Force out = Force in x (arc of force in / arc of force out)

The less the output end moves respect to the input end, the greater the output force is.
If you could experiment with each of the two shapes that you have shown, you could see that the length of the described arcs are exactly the same in both cases.

Therefore, size matters, but shape does not.