I Maximum likelihood w/ histogram, zero probability samples

[FrankJ777]

I'm trying to replicate a machine learning experiment in a paper.The experiment used several signal generators and "trains" a system to recognize the output from each one. They way this is do is by sampling the output of each generator, and then building histograms from each trial. Later you are supposed to be able to sample a generator randomly and use Maximum likelihood to determine which generator the output is from. This is done by comparing the samples to the histograms to determine the probability of each sample, and then multiplying the probabilities of each occurrence. I think the formula is this:

ML = (P=x1)(P=x2)(P=x3)...(P=xn)

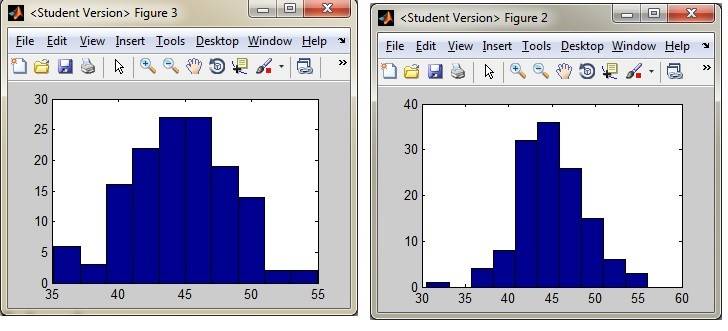
So referring to the histograms below, if I received a sample set of say, [ 35, 40, 45 ,45, 46, 50] i would calculate the ML for each by finding the bin they belong to in each histogram to determine they're probability and multiplying each.

Assuming 134 samples:
ML (fig 3) = (5/134) * (15/134) * (26/134) * (26/134) * (26/134) * (15/134)

Assuming 123 samples:
ML (fig 2) = 0 * (7/123) * (35/123) * (35/123) * (35/123) * (15/123)

It seems that in the second case my ML would go to 0. But this doesn't seem like an unlikely event, it just didn't happen during the training phase. In fact it would seem that outliers could make the ML go to zero in that case. Even if I used the log of probabilities log(0) is indeterminate. So am I doing this correctly, or do I not understand the method. I'm new to this concept so I would appreciate if someone could shed some light on what I don't understand. Thanks.

Here's the link to the relevant paper by the way.
https://www.google.com/url?sa=t&rct...es.pdf&usg=AFQjCNFy9xsSBifMiHIqESYdQ494XOlvzQ

 

[mfb]

An interesting problem. Maximum likelihood would only work exactly if your histogram is perfect. In this case, 0 would really mean this emitter can be excluded. With a finite sample as approximation, that doesn't have to be true, of course.

- You can try to estimate the "true" shape based on your histogram: Fit some smooth function to the histogram.
- You can create confidence intervals in each bin, and then take the upper limits for all bins to make a new histogram. This will weaken your separation power, but I think this is correct, as you do not know the true distribution exactly.
- You can do the analysis unbinned and define the likelihood based on the distance to events in the training sample. A similar problem arises in particle physics in searches for CP violation in Dalitz plots. k-nearest neighbor is one of the methods used there.
- While introducing Bayesian statistics would probably work, I'm not sure if it would help.

 

[Stephen Tashi]

Assuming 134 samples:
ML (fig 3) = (5/134) * (15/134) * (26/134) * (26/134) * (26/134) * (15/134)

That doesn't look like a calculation for the probability of the sample.

Take the simplified case of 3 bins where the empirical historgram of the bins has counts [7][1][2].
Suppose a sample of data has 4 observations whose membership in the bins is: 1,2,2,3.

Taking the histogram as the probability distribution, the joint probability of the 4 observations (assuming they are independent events) is P = (7/10)(1/10)(1/10)(2/10). That is the "liklihood" of the sample.

The term "maximum liklihood" only applies if you have several different histograms. The histogram that gives you the maximum probability for the sample is the "maximum liklihood" estimate for which historgram generated the data.

 

[FrankJ777]

Thanks mfb. I'm going to play around with a couple of your suggestions. I'm new to ML, but from what I've read it seams to be common in machine learning. What I'm not sure about is how the situation of "outlying" data-points is handled. It seems to me that ML is intended to determine what known distribution a sample has been chosen from. So even though a new sample from the same transmitter with a very similar distribution, could have an outlier that is outside of the training data limits, in which case the ML would go to 0.

 

[FrankJ777]

That doesn't look like a calculation for the probability of the sample.

Hi Stephen. That's exactly what its supposed to be is Maximum likelihood. The two histograms are data samples from two different transmitters, and the "new" sample is from and unknown transmitter that I'm trying to see if it likely came from either of the two transmitters.