Measure the acceleration due to gravity on a distant planet

[rayhan619]

Homework Statement

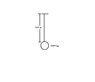
To measure the acceleration due to gravity on a distant planet, an astronut hangs a 0.055 kg ball from the end of a wire. the wire has a length of 0.95 n and a linear density of 1.2*10
^-14 kg/m. using electronic equipment, the astronaut measures the time for a transverse pulse to travel the length of the wire and obtains a value of 0.016 s. the mass of the wire is negligible compared to the mass of the ball.
a) draw a nice picture
b) calculate the velocity of the pulse
c)determine the acceleration due to gravity

Homework Equations

f = v/2L
v = (Mg/mu)^sq. root

The Attempt at a Solution

m = 0.055 kg
L = 0.95 m
mu = 1.2*10^-4 kg/m
T = 0.016 s

b)f = 1/0.016s = 62.5 hz
v = 2fL = 2*62.5 hz*0.95 m = 118.75 m/s

c)g = (v^2*mu)/M = {(118.75 m/s)^2*1.2*10^-4 kg/m}/0.055 kg = 30.77 m/s^2

i got both of them wrong. where did i screw up?

 

[Doc Al]

b)f = 1/0.016s = 62.5 hz
v = 2fL = 2*62.5 hz*0.95 m = 118.75 m/s

This is a pulse, not a standing wave. The speed of the pulse is simply distance/time.

 

[rayhan619]

a) i have attached the picture to check it.

so for b) v = L/t = 0.95 m/ 0.016 s = 59.38 ms^-1

and c) g = {(59.38 m/s)^2 * 1.2*10^-4 kg/m}/ 0.055 kg = 7.69 m?s^2.

right?

 

[Doc Al]

Looks good to me.

 

[rayhan619]

appreciate it man