- #1
feynmansorange
- 2
- 0
- Homework Statement
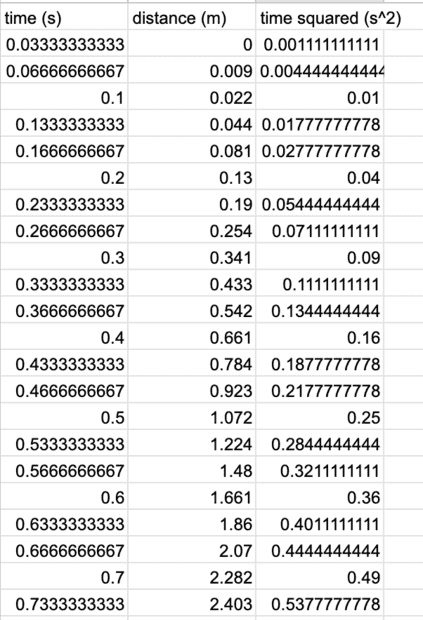
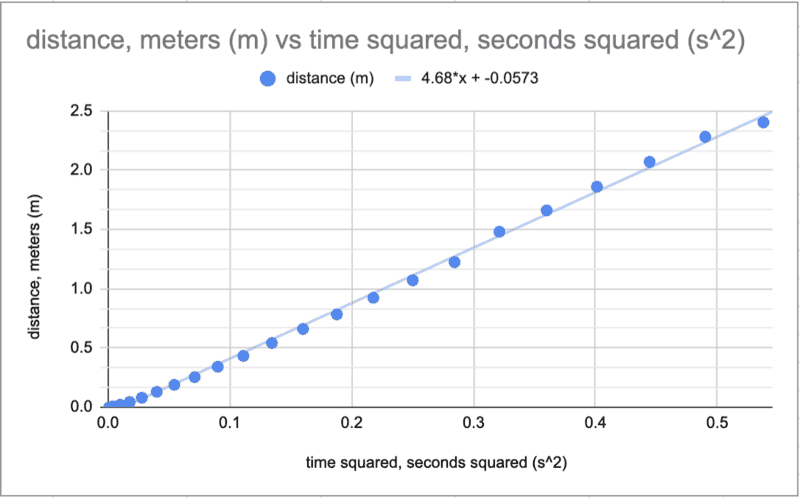
- Hi! I'm doing a lab where my class is verifying the acceleration due to gravity. We dropped an object and recorded the time with a spark timer, then measured the meters every 1/30th of a second. So, I have distance (meters) and time (seconds). THEN we square the time, and plot that on a graph of dist. vs time^2. But my slope is only roughly half of gravity??? isn't the acceleration supposed to be equal to gravity?
- Relevant Equations
- s=ut+1/2at^2
Data and graphs here (the time is measured every 1/30 of a second, but for some reason, Google Sheets thought 1/30 wasn't a number so its in decimals!!! very confusing!!! so sorry about that!). why is the slope only 4.68, should it not be 9.81m/s^2? is the slope of m/s^2 not supposed to be acceleration due to gravity? is my data weird? thanks!