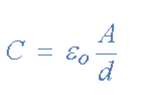SUMMARY
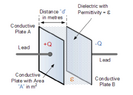
The discussion focuses on measuring the capacitance variation of a self-made capacitor in response to sound waves. The relationship between capacitance (C), permittivity (ε0), area (A), and distance (d) is established, with ε0 and A remaining constant. Participants suggest using a De Sauty Bridge for measurement, although it may not meet all requirements. A practical method involves charging the capacitor to a DC voltage, disconnecting the source, and measuring the resulting AC voltage as the plate separation changes due to sound waves, utilizing a FET follower as a voltage buffer.
PREREQUISITES
- Understanding of capacitance and its formula C = ε0 * A / d
- Familiarity with FET (Field Effect Transistor) operation
- Knowledge of AC and DC voltage measurement techniques
- Basic principles of sound wave propagation and its effects on physical systems
NEXT STEPS
- Research the design and application of a De Sauty Bridge for capacitance measurement
- Learn about FET follower circuits and their use as voltage buffers
- Explore methods for measuring AC voltage in capacitive systems
- Investigate the principles of sound wave interaction with electrical components
USEFUL FOR
Electronics enthusiasts, experimental physicists, and engineers interested in capacitive sensing and sound wave measurement techniques.