- #1
Hindsigh101
- 2
- 0
0. Bit o' background + greeting
Hello everyone. I am a third-year math/physics/CS/AI major and I've never used this forum before, as can be seen from my impressive post count. I enjoy leafing through it though and find myself perpetually impressed by the activity and commitment of the community. I could not find an answer to what I want to know on the net, so I was hoping you guys could delve into your physics-wisdom-hats and help me out.
I am helping a teacher by trying to devise an experiment to be carried out by two first-year physics students. Note that this means I will not get graded on its design or execution.
As stated in the title, the aim of the experiment is to determine the frequency-dependency of the resistance of a coil inductor using rudimentary equipment. In all this, the coil is modeled as a perfect inductor in series with a (small) resistance and parallel to a perfect capacitor representing the parasitic capacitance. I know that there are devices that can do this fairly easily and with some more (unavailable) math it could even be done with a simple bridge. The students only have access to the following:
- All sorts of garden-variety capacitors and resistors
- AC current up to 1.4 MHz or something like that
- Oscilloscope
- Multimeter
- Wheatstone bridge
My question is: Do you know of a creative or conventional method of measuring this dependency?
Althought measuring and graphing the resistance will constitute the experiment and is therefore where I would appreciate help the most, it would be nice to have some reasonable theoretical foundation for all this. This would also provide us with a means of determining the accuracy of the measurements performed by fitting some data. I know that most of the frequency-depency comes from the skin- and proximity-effect that inductors suffer from and I can explain these effects qualitatively. However, there might be other things to consider.
Question for bonus points: Does there exist a (not necessarily pretty) analytical/approximate expression for the resistance based on the dimensions and materials of the coil that is useful for simple coils?
I can't imagine that such an expression doesn't exist, what with all the audio-equipment designers perfecting their amplifiers.
I am not sure what to put here exactly. My main question is about the experiment, the theory behind it is just gravy. Putting equations here will make this post a tad big, which could be destracting and demotivating. You all know the basic impedance/frequency response relations, so I see no point in reiterating them here. I suppose I could provide you with some equations governing the http://en.wikipedia.org/wiki/Skin_effect" seperately. From wikipedia:
For the skin-effect:
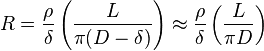
where δ is the skin depth.
For the proximity-effect:
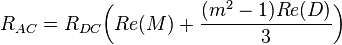
where D and M are complicated expressions involving inductor-specific variables and the frequency.
Note: I used images because the images generated by the tex expressions I made seemed to be stored in memory and were wrong every time I previewed this post =/
The first idea I had was to use the fact that the height of the peak of the frequency-response of a series RLC-circuit at the resonance frequency is governed only by the resistance of the connected resistor and that of the inductor (disregarding all other resistances). This will obviously only work if the resistance of the inductor becomes high enough to reasonably ignore all other resistances. Also, the resistor shouldn't be too big as to overshadow the resistance of the coil. The idea is to hook up parallel capacitors with varying capacitance to move the resonance frequency around, measure the response at each resonance frequency and calculate the contribution of the resistance of the coil. Some consideration must be put into choosing the right components so the peak is well-defined, but not too sharp, making it hard to find because of the coarseness of the AC generator.
While this may work, I just have the horrible feeling that this experiment is too crude to actually provide a reasonable result. The difference in resistance might only be noticable at considerably high frequencies and at that point I can't be sure that some other components aren't throwing me off course. This is actually the main problem I have with coming up with a way of measuring it: I don't have a good enough overview of all the odd stuff happening in a circuit at high frequencies. Hopefully some of you can shed some light on how to go about doing this using your experience in working with circuits.
Thank you in advance!
Hello everyone. I am a third-year math/physics/CS/AI major and I've never used this forum before, as can be seen from my impressive post count. I enjoy leafing through it though and find myself perpetually impressed by the activity and commitment of the community. I could not find an answer to what I want to know on the net, so I was hoping you guys could delve into your physics-wisdom-hats and help me out.
I am helping a teacher by trying to devise an experiment to be carried out by two first-year physics students. Note that this means I will not get graded on its design or execution.
Homework Statement
As stated in the title, the aim of the experiment is to determine the frequency-dependency of the resistance of a coil inductor using rudimentary equipment. In all this, the coil is modeled as a perfect inductor in series with a (small) resistance and parallel to a perfect capacitor representing the parasitic capacitance. I know that there are devices that can do this fairly easily and with some more (unavailable) math it could even be done with a simple bridge. The students only have access to the following:
- All sorts of garden-variety capacitors and resistors
- AC current up to 1.4 MHz or something like that
- Oscilloscope
- Multimeter
- Wheatstone bridge
My question is: Do you know of a creative or conventional method of measuring this dependency?
Althought measuring and graphing the resistance will constitute the experiment and is therefore where I would appreciate help the most, it would be nice to have some reasonable theoretical foundation for all this. This would also provide us with a means of determining the accuracy of the measurements performed by fitting some data. I know that most of the frequency-depency comes from the skin- and proximity-effect that inductors suffer from and I can explain these effects qualitatively. However, there might be other things to consider.
Question for bonus points: Does there exist a (not necessarily pretty) analytical/approximate expression for the resistance based on the dimensions and materials of the coil that is useful for simple coils?
I can't imagine that such an expression doesn't exist, what with all the audio-equipment designers perfecting their amplifiers.
Homework Equations
I am not sure what to put here exactly. My main question is about the experiment, the theory behind it is just gravy. Putting equations here will make this post a tad big, which could be destracting and demotivating. You all know the basic impedance/frequency response relations, so I see no point in reiterating them here. I suppose I could provide you with some equations governing the http://en.wikipedia.org/wiki/Skin_effect" seperately. From wikipedia:
For the skin-effect:
where δ is the skin depth.
For the proximity-effect:
where D and M are complicated expressions involving inductor-specific variables and the frequency.
Note: I used images because the images generated by the tex expressions I made seemed to be stored in memory and were wrong every time I previewed this post =/
The Attempt at a Solution
The first idea I had was to use the fact that the height of the peak of the frequency-response of a series RLC-circuit at the resonance frequency is governed only by the resistance of the connected resistor and that of the inductor (disregarding all other resistances). This will obviously only work if the resistance of the inductor becomes high enough to reasonably ignore all other resistances. Also, the resistor shouldn't be too big as to overshadow the resistance of the coil. The idea is to hook up parallel capacitors with varying capacitance to move the resonance frequency around, measure the response at each resonance frequency and calculate the contribution of the resistance of the coil. Some consideration must be put into choosing the right components so the peak is well-defined, but not too sharp, making it hard to find because of the coarseness of the AC generator.
While this may work, I just have the horrible feeling that this experiment is too crude to actually provide a reasonable result. The difference in resistance might only be noticable at considerably high frequencies and at that point I can't be sure that some other components aren't throwing me off course. This is actually the main problem I have with coming up with a way of measuring it: I don't have a good enough overview of all the odd stuff happening in a circuit at high frequencies. Hopefully some of you can shed some light on how to go about doing this using your experience in working with circuits.
Thank you in advance!
Last edited by a moderator: