Mechanical Deformation: Rubber Ball & Cylinder Experiment

[somasimple]

Hello All,

Here is my asking:

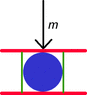
A rubber ball (blue) is put between two horizontal planes (in red).
There is also a deformable cylinder (green) around my ball and this cylinder is filled with water (the cylinder contains the ball and water).

1/If a force/mass is applied on the top of the upper plate, is there some force deviated in the cylinder horizontally?
2/ Is the applied force, in part, suppressed verticallly?

 

[Q_Goest]

If the top plate moves down, the green sides will bulge outward. The amount is dependant on the ball. The ball could be solid throughout or it could have an air/gas filled cavity inside. The question is, "Is the ball incompressible like the water or not?".

If it's incompressible like the water, then the volume of the liquid & ball filled cavity will remain relativly constant. The only reduction in volume will be because of the water and ball's bulk modulus as the material increases density very slightly with pressure. To determine how much deformation you get you can safely ignore the slight increase in density due to pressure and assume it is incompressible because the error incurred is going to be very small compared to errors in measurement. Then the volume stays constant and the movement downward of the top plate must be compensated for by the green walls bulging out.

If the ball is not incompressible, if it is more like a tennis ball with air or a gas inside, there are other things to consider. If the pressure inside the ball is higher than the surroundings, the skin of the ball is in tension and the ball won't reduce in volume until the surrounding pressure exceeds the internal pressure plus whatever structural support is provided by the skin. In this case the volume of the contents stays constant just like above and you can assume the contents are incompressible.

However, if the ball is more like a balloon, the ball will shrink with increasing pressure, but in proportion to the pressure. The result is the sides bulge out less than if the ball were incompressible because of the reduction in volume of the ball.

The applied force is "suppressed" vertically. Since the pressure is assumed to increase as the sides deform, that increased pressure must be countered by an increased force. Note that the pressure increases because we are assuming the green walls are deformable but have some structural strength.

 

[somasimple]

Thanks for this complete response that went further my thoughts.

I made another picture showing the deformation.
a/ the ball is solid/homogeneous but deformable.
b/ water fills completely the resting volume.
c/ we suppose that they are not relly compressible as you said it.

If I have understood, the walls are curved by the vertical force but the it is damped by this deformation?

Some more questions.
1/If there is no left space in the container, could we say that force is applied uniformly on the top (water and ball)?
2/ If there is a little loss of water, could we say that force is thus more applied on ball?
3/ In the 2 previous conditions 1 et 2, could we say that the second one allows more inclination of the plate if the forece is applied more laterally?

 

[Q_Goest]

If I have understood, the walls are curved by the vertical force but the it is damped by this deformation?

Is it damped? Yes. As the chamber deforms, the water adjusts to the new shape and must flow in order to do so. The flow of a liquid results from a slight pressure gradient in the fluid. If there were no pressure gradient, the fluid wouldn't flow and the chamber couldn't change shape. The flow of fluid dissipates energy and creates heat, just as it would in a shock absorber, though in this case the difference in pressure within the chamber is slight so the amount of energy dissipated and the amount of damping in comparison to a shock absorber is small. Note that if the movement is extremely slow, the pressure difference is similarly small, so the more slowly one compresses, the less damping there is also.

1/If there is no left space in the container, could we say that force is applied uniformly on the top (water and ball)?

I think you're asking, if the ball is touching the top and bottom of the container, is the force of the ball and the force of the water uniform across the inside surface of the container. Is that correct? If so, the answer is no, a ball will have some modulus of elasticity to it, so the force on the top inside surface of the container where the ball meets it is very roughly the sum of the internal pressure plus the ball's force from deformation. Where the ball is not contacting the inside surface, only the pressure of the water is pushing upward. It may be hard to visualize the idea that the contact pressure between the ball and container is the sum of the water plus deforming force of the ball so if that seems confusing I'll try and elaborate if you want.

2/ If there is a little loss of water, could we say that force is thus more applied on ball?

Yes, as the water is removed under pressure, the sides move back toward the original, unpressurized position, so the pressure of the water decreases, while the ball still maintains its structural support. Note above, the contact between the ball and inside surface is the sum of the water pressure and the ball's force upward, so as water is removed and pressure decreases, a larger percentage of load is applied by the ball.

3/ In the 2 previous conditions 1 et 2, could we say that the second one allows more inclination of the plate if the forece is applied more laterally?

Not sure what you mean here, sorry.

 

[somasimple]

Thanks for this clear reponse.

My understanding is now:
1/ Damping occurs only if force is quick, if not, it is more "transmitted" to the lower plate.

It may be hard to visualize the idea that the contact pressure between the ball and container is the sum of the water plus deforming force of the ball so if that seems confusing I'll try and elaborate if you want.

It is hard to visualize!
2/ Do you mean that if the ball was surrounded by water thus it will receive less pressure than water?

Not sure what you mean here, sorry.

I made a picture showing my question.

I think that if in normal condition if water fills completely the left space, it does not allow an high inclination. The movement is stopped by internal pressure and wall resistance and ball.
If you remove some water, the inclination will go further?