Mechanical Principals Assignment Question

[Al_Pa_Cone]

I have a long question in my assignment with many part answers and I would just like to know if I have answered them correctly as I have spend a lot of time on it. can anyone help?

My Question is:

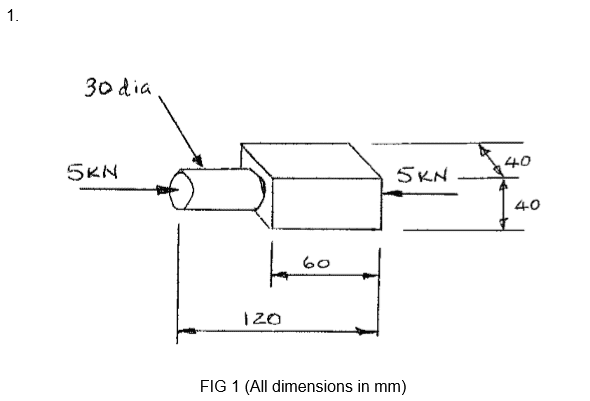
The component shown in Fig 1 is made from a material with the following properties and is subjected to a compressive force of 5kN.

Material Properties
Young’s Modulus of -200 GN m^-2
Elasticity Modulus of Rigidity -90 GN m^-2
Poisons ratio - 0.32Q1a. Calculate the stress in:

(i) the circular section

(ii) the square section

My Solution:

Does This Look Correct?

Q1b. Calculate the strain in:

(i) The circular section

(ii) The square section

Does This Look ok?

Q1c. The change in length of the component

Q1d. The change in diameter of the circular section

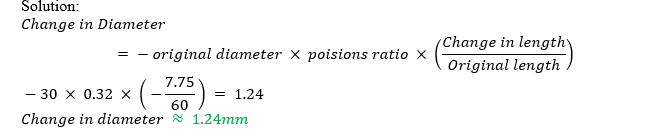
Q1e. The change in the 40mm dimension on the square section

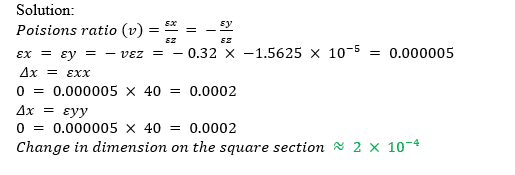
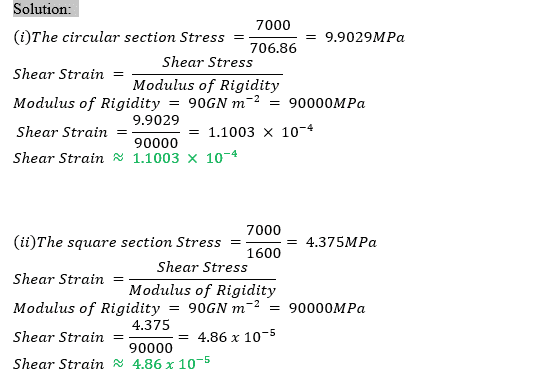
Q1f. If the same component were subjected to as shown in FIG 2, calculate the shear strain in:

(i) The Circular section
(ii) The Square section

Any help or advice would be much appreciated. Thanks

 

[mjc123]

1a. Looks OK to me.
1b. Wrong units for strain. Strain is dimensionless (and in this case negative).
1c. Be careful with signs and units. 0.002121 is not equal to -2.121 x 10^-3. And -2.121 x 10^-3 what? You are mixing units too much, and getting confused. I would convert everything into m (and Pa etc.)
1d. Change in length is not 7.75. What length is being referred to? (Why don't you just do it like 1e?)
1e. OK, but what are the units of the answer?
1f. As there is no Fig 2, this is impossible.

 

[Al_Pa_Cone]

Thanks for your help, I rushed the first part of the assignment because I was working to a deadline. That deadline was removed and now I have more time to think.
I have reworked Q1a although you said it was ok, I couldn't work out how I got the area values I had wrote down and also my answers are now positive? should they be Negative?

 

[mjc123]

No, you had it right the first time. A uniaxial stress is applied in the z direction. There is no applied stress in the x or y directions. The area to use is $\pi$r² or wl. And a compressive stress is negative. (And areas don't have units of mm³. And 1000 mm³ is not 1 m³, nor is 1000 mm² 1 m². You are causing yourself a lot of unnecessary problems simply by being sloppy.)

 

[Al_Pa_Cone]

I have used the area previously used and obtained a figure the same but I still have a unit measurement difference. I am not sure the first unit of MPa was correct because of the conversion of mm into m. Previously I calculated m from mm by x10^-6 when it should have been x 10^-3. Am I correct in this error?

 

[Al_Pa_Cone]

(And areas don't have units of mm3. And 1000 mm3 is not 1 m3, nor is 1000 mm2 1 m2. You are causing yourself a lot of unnecessary problems simply by being sloppy.)

1000mm does equal 1 meter?

 

[Al_Pa_Cone]

Ahh I see my problem! 1.6^2 = 2.56 where 1600^2 = 2560000 which is x10^-6. Looks like I have answered my own question there. Sorry about that, I was thinking out loud!

 

[mjc123]

Yes, but 1000 mm² does not equal 1 m². Just picture a circle 30 mm in diameter. Do you think its area is anywhere near 1 m²?

 

[Al_Pa_Cone]

Does this look ok for part b?

 

[mjc123]

You are mixing units again! That's -7.074 MPa/200 GPa = -0.0354 x 10^-3! You got it right (apart from the sign) in part c - 3.3535 x 10^-5

 

[Al_Pa_Cone]

Does This look better?

 

[Al_Pa_Cone]

Reworked part c

 

[mjc123]

That looks better. But what's with all the ≈ signs? You're asked to calculate a value, not estimate an approximate value. I would calculate it precisely, then round to the appropriate number of significant figures at the end.

 

[Al_Pa_Cone]

I must be mistaken but I thought my use of the algibraic ≈ was suitable for my final answer. I have used it in previous assignments which were marked with distinction but never mentioned. I will stick with the standard = in future.

When you said calculate it precisely, then round to the appropriate number of significant figures at the end. I understand it effects my final answer, but do you think my answer is not accurate enough to be accepted on this occasion?

 

[mjc123]

Considering the numbers you were given, I think 2 sig figs is OK for an answer, but if you're going on to use those results in other calculations, you should use the more precise values for that purpose.

 

[Al_Pa_Cone]

Reworked answers to D and E?

 

[mjc123]

d. Poisson's ratio is positive, so the diameter increases.
e. Wrong - you have used the change in length instead of the strain.

 

[Al_Pa_Cone]

Material Properties
Young’s Modulus of -200 GN m^-2
Elasticity Modulus of Rigidity -90 GN m^-2
Poisons ratio - 0.32

From the Question given, It shows the Poissons ratio to be Negative? I undertand a compression on the top of a cylinder would increase the diameter of the midsection but how would I change the given figure to suit this answer?

If I remove the negative symbol my previous workings for part d, I get the same answer but as a positive. Is this acceptable?

and for part 'e'my reworkings are:

 

[Al_Pa_Cone]

1a. Looks OK to me.
1b. Wrong units for strain. Strain is dimensionless (and in this case negative).
1c. Be careful with signs and units. 0.002121 is not equal to -2.121 x 10^-3. And -2.121 x 10^-3 what? You are mixing units too much, and getting confused. I would convert everything into m (and Pa etc.)
1d. Change in length is not 7.75. What length is being referred to? (Why don't you just do it like 1e?)
1e. OK, but what are the units of the answer?
1f. As there is no Fig 2, this is impossible.

In your first post you said '(Why don't you do it like in 1e?)'

So here is my answer in the same method as 1e and it is positive, and different from my previous calculation.

 

[mjc123]

I think you are confusing dashes with minus signs. Do you think the Young's modulus is -200 GPa? You haven't used a negative value in your calculations! Poisson's ratio for ordinary materials is positive. When you compress them uniaxially, they expand in the transverse directions. (There are a few exotic materials which have a negative PR, with niche applications.)
What are you doing in part e? You have replaced the change in length with the strain, but you get the same (wrong) answer as before! Didn't you redo the calculation?

 

[Al_Pa_Cone]

I think you are absoloutly correct! I am that concerned with trying to take all of this new information in, I am overlooking an obvious fact. It is poorly set out in the assignment but I should have noticed that anyway!

So as it stands in part d , is my orignial method of working out correct with the correct poissons ratio?

 

[Al_Pa_Cone]

What are you doing in part e? You have replaced the change in length with the strain, but you get the same (wrong) answer as before! Didn't you redo the calculation?

I did Re-do the calculation but I noticed I had missed out the multiplication of z in this equation

Also It shows in this equation that v (Poissons Ratio) is a negative figure which makes the answer a positive figure?

Can you recommend another method I should use?

 

[mjc123]

You have a spurious negative sign on the RHS, but the green answer is correct.

 

[Al_Pa_Cone]

How about this for e?

 

[mjc123]

Why have you included x60? $\epsilon x = -\nu\epsilon z$ = -0.32 x -1.55 x 10^-5 That is your x strain. You multiply that by the width to get the change in width. You got it right the first time!

 

[Al_Pa_Cone]

1a. Looks OK to me.
1b. Wrong units for strain. Strain is dimensionless (and in this case negative).
1c. Be careful with signs and units. 0.002121 is not equal to -2.121 x 10^-3. And -2.121 x 10^-3 what? You are mixing units too much, and getting confused. I would convert everything into m (and Pa etc.)
1d. Change in length is not 7.75. What length is being referred to? (Why don't you just do it like 1e?)
1e. OK, but what are the units of the answer?
1f. As there is no Fig 2, this is impossible.

As for Question 1f, I assume I have a running pattern of being completely wrong, but here is the FIG 2 I failed to initially post.

And my Answer?

 

[mjc123]

Looks correct to me.

 

[Al_Pa_Cone]

Great! I am just working bac through my assignment now and correcting where I have made mistakes.
I have one more Question if you could help me? it is only a 1 part question but I have a Negative answer for my Bulk modulus? I am not sure I should have a Negative answer.

My Answer is:

 

[mjc123]

Careful with units again here! The volume is 5.24 x 10⁵ mm³ - not m³. Fortunately in ΔV/V the units cancel out. Its value is -3.817 x 10^-3 NO UNITS!
You have missed out a negative sign from the definition of bulk modulus. When you compress a body the volume decreases, so the bulk modulus is defined as
K = -VdP/dV
1047.94 MPa is the right answer (but too many sig figs), but this is not equal to 1.5 GPa but 1.05 GPa.
I don't want to sound hectoring, but as I said before you are making problems for yourself by being careless. One characteristic of a good scientist or engineer is attention to detail. Be careful about copying equations and calculations accurately, including signs. And pay careful attention to units. Get into the habit of thinking of a quantity as number plus unit, not just number (unless it happens to be dimensionless). It is never right to say that e.g. the length is 10. 10 what? metres, mm, miles, Angstroms? And be careful about mixing units, e.g. dividing MPa by GPa. It may be helpful to write the units in your calculation, e.g. 7 MPa/200 GPa rather than 7/200 and try to remember to correct for the conversion factor. Or convert everything to the same units before doing the calculation.

 

[Al_Pa_Cone]

I can't thank you enough for your help with all of this. This time last year I was just starting the course and I have had to learn everything from scratch. I hadnt touched algebra in 16 years and there was no explanation behind the reason why engineers use x10^3 as apposed to x1000. I have learned most of the methods I use by searching outside of the e learning and sifting through forums and youtube videos, Therefore there have been gaps in my education hence the reason I make mistakes a lot.
I have a hundred questions I could ask you but I won't take up all of your time. Thanks again for your help!