Complex Loading Systems And Loaded Beams And Cylinders

[Willc96]

Hello this is my first post here so basically I've had my best crack at all the questions all I am really after is a bit or re assurance as to my answers and if any are wrong were I have gone wrong essentially. I've tried to include all my working out were possible.

1. Homework Statement

The component shown in Fig 1 is made from a material with the following properties and is subjected to a compressive force of 5kN.

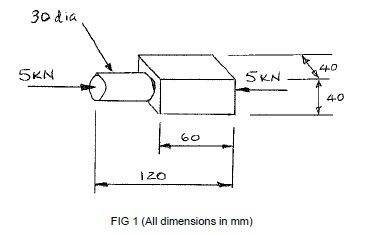
Material Properties :
Young’s Modulus of Elasticity – 200 GNm ^{- 2}
Modulus of Rigidity – 90 GNm ^{- 2}
Poisons ratio – 0.32

2. Homework Equations

Calculate :
(a) The stress in :
(i) the circular section
(ii) the square section

(b) The strain in :
(i) The circular section
(ii) The square section

(c) The change in length of the component

(d) The change in diameter of the circular section

(e) The change in the 40mm dimension on the square section

(f) If the same component were subjected to a shear force of 7 kN as shown in FIG 2, calculate the shear strain in :

(i) The circular section
(ii) The square section

3. The Attempt at a Solution

Calculate :
(a) The stress in :
(i) the circular section

Stress = Force / Area
Area of circular section = πr²
π(15)² = 706.8583mm²
Answer : Stress = 5000 / 706.86 = - 7.07MPa

(ii) the square section

Stress = Force / Area
Area of the square section = length x height
40 x 40 = 1600mm²
Answer : Stress = 5000 / 1600 = - 3.125MPa

(b) The strain in :
(i) The circular section

ε = dl / l₀ = σ / E
σ = F / A = 7.07MPa
E = 200GN / m ^{- 2} = 200000MPa
7.07 / 200000 = 0.00003535
Answer: Strain = - 3.535 x 10 ^{- 5}

(ii) The square section

ε = dl / l₀ = σ / E
σ = F / A = 3.125MPa
E = 200GN / m ^{- 2} = 200000MPa
3.125 / 200000 = 0.000015625
Answer: Strain = - 1.5625 x 10 ^{- 5}

(c) The change in length of the component

ε = dl / l₀

For the Cylinder Section
ε = 3.535 x 10 ^{- 5}
l₀ = 60
dl = ε x l₀
dl = 3.535 x 10 ^{- 5} x 60 = 0.002121
= - 2.121 x 10 ^{- 3}

For the Square Section
ε = 1.5625 x 10 ^{- 5}
l₀ = 60
dl = ε x l₀
dl = 1.5625 x 10 ^{- 5} x 60 = 0.005625
= - 5.625 x 10 ^{- 3}

Adding the two changes together
- 2.121 x 10 ^{- 3} + - 5.625 x 10 ^{- 3}
= - 0.007746
Answer Change in Length = - 7.75mm

(d) The change in diameter of the circular section

Change in Diameter = - original diameter x poisions ratio x (Change in length / Original length)
- 30 x 0.32 x ( - 7.75 / 60 ) = 1.24
Answer Change in diameter = 1.24mm

(e) The change in the 40mm dimension on the square section

Poisions ratio (v) = ε_x / ε_z = - ε_y / ε_z
ε_x = ε_y = - vε_z
= - 0.32 x -1.5625 x 10 ^{- 5}
= 0.000005
Δx = ε_xx₀ = 0.000005 x 40 = 0.0002
Δx = ε_yy₀ = 0.000005 x 40 = 0.0002
Answer Change in dimension on the square section
= 2 x 10 ^{- 4}

(f) If the same component were subjected to a shear force of 7 kN as shown in FIG 2, calculate the shear strain in :

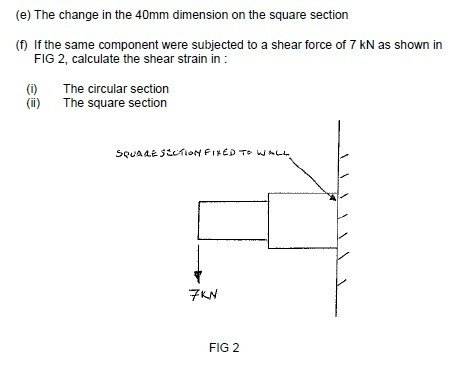
(i) The circular section

Stress = 7000 / 706.86 = 9.9029MPa
Shear Strain = Shear Stress / Modulus of Rigidity
Modulus of Rigidity = 90GN/m ^{- 2}
= 90000MPa
Shear Strain = 9.9029 / 90000 = 1.1003 x 10 ^{- 4}
Answer Shear Strain = 1.1003 x 10 ^{- 4}

(ii) The square section

Stress = 7000 / 1600 = 4.375MPa
Shear Strain = Shear Stress / Modulus of Rigidity
Modulus of Rigidity = 90GN/m ^{- 2}
= 90000MPa
Shear Strain = 4.375 / 90000 = 4.86 x 10 ^{- 5}
Answer Shear Strain = 4.86 x 10 ^{- 5}

 

[Willc96]

* Edit

Homework Equations

[/B]
Stress = Force / Area
ε = dl / l0 = σ / E
Shear Strain = Shear Stress / Modulus of Rigidity
Poisions ratio (v) = εx / εz = - εy / εz

 

[Willc96]

Anyone ?