Mechanics-Diff equation problem

[kof9595995]

Yesterday my friend asked me: what will happen if a force F with constant magnitude is applied to one end of a free stick(no other force), and this force F is always normal to the stick.
He told me it's not a textbook problem and he just asked out of curiosity，so I decide not to put this thread in homework section, but still I'll show my attempt to the solution.
Suppose the stick is uniform with length l and mass M

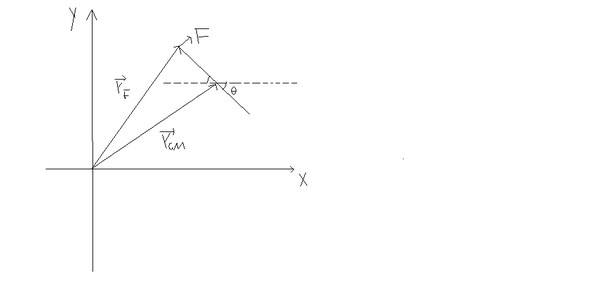
Let's denote the position of center of mass as
$$\[\overrightarrow {{r_{cm}}} = (x,y)\]$$
The angle rotates over is $$\[\theta \]$$
then the point that the force applied at is
$$\[\overrightarrow {{r_F}} = (x - \frac{l}{2}\cos \theta ,y + \frac{l}{2}\sin \theta )\]$$
I choose the axis of rotation to be the axis perpendicular to the paper and passing thru the origin,and we know force is
$$\[\overrightarrow F = (F\sin \theta ,F\cos \theta )\]$$
then I can express torque as
$$\[\overrightarrow \tau = \overrightarrow {{r_F}} \times \overrightarrow F = F(x\cos \theta - y\sin \theta - \frac{l}{2})\hat k\]$$
About the moment of inertia I apply the parallel axis theorem
$$\[I = {I_{cm}} + M{D^2} = \frac{1}{{12}}M{l^2} + M({x^2} + {y^2})\]$$
Now we can just apply Newton's law:
$$\[\left\{ \begin{array}{l} \ddot x = \frac{F}{M}\sin \theta \\ \ddot y = \frac{F}{M}\cos \theta \\ \ddot \theta = \frac{{|\overrightarrow \tau |}}{I} = \frac{F}{M}\frac{{x\cos \theta - y\sin \theta - \frac{l}{2}}}{{\frac{{{l^2}}}{{12}} + {x^2} + {y^2}}} \\ \end{array} \right.\]$$
Then I'm totally stuck, I'm not that optimistic to expect an exact solution but the embarrassing thing is I can't even reduce the system to a single variable diff equation.
Can anybody help me reduce this? Any help is appreciated. Of course if somebody tells me there's an exact solution， I‘ll be happy enough to have a party.
(I checked these equations one time and hopefully no mistake. )

 

[Marin]

Hi there!

It is indeed an interesting problem :)

In general, trying to solve any mechanical system of ODEs, first try to find the integrals of motion of the system (if there are any), i.e. the conserved quantities (energy, generalised momenta). This often reduces the 2.nd order ODEs to 1.st order ODEs.

You have made a good choice of origin, except for the discription of the rotation. Hence, I think there's a mistake in the third equation of your system:

Here are some well-known identities:

$$L=J\dot\theta$$

$$\dot L=M$$
$$M=F\frac{l}{2}$$

we do not need them in vector notation since the constant force is always normal to the stick (J is the moment of inertia, M is the torque and L the angular momentum)

You have to always be careful with the choice of frame of reference. Observe that the torque equals the time derivative of the entire angular momentum. As your calculations are absolutely correct, it follows:

$$M=\dot L=\frac{d}{dt}(J\dot\theta)=\dot J\dot\theta+J\ddot\theta=\frac{d}{dt}(\frac{1}{12}ml^2+m(x(t)+y(t)))\dot\theta+J\ddot\theta\neq J\ddot\theta$$

so the 3rd. equation does not hold any more.


I would suggest to choose the axis of rotation in the centre of mass, so that you obtain a simple equation for theta (you won't need the parallel axis thm. )


As to the system itself, you can go polar writing:

$$\vec r=(x,y) = (r\cos\phi,r\sin\phi)$$, $$r^2=x^2+y^2$$

then, it follows for the torque using the first two equations:

$$M = F(x\cos\theta-y\sin\theta-l/2)=F(m/Fx\ddot y-m/Fy\ddot x-l/2)=m(x\ddot y+\dot x\dot y-\dot y\dot x-y\ddot x)=m\frac{d}{dt}(x\dot y-y\dot x)$$

further, using the defs for x and y via r and phi we obtain:

$$m\frac{d}{dt}(x\dot y-y\dot x)=m\frac{d}{dt}(r\dot r\sin\phi\cos\phi+r^2\dot\phi\cos^2\phi-r\dot r\cos\phi\sin\phi+r^2\dot\phi\sin^2\phi)=m\frac{d}{dt}(r^2\dot\phi)$$

$$M=m\frac{d}{dt}(r^2\dot\phi)$$

but we also know that: $$M=\dot L=\frac{d}{dt}(J\dot\theta)=m\frac{d}{dt}(r^2\dot\phi)$$

=> $$mr^2(t)\dot\phi(t)=J(t)\dot\theta(t)$$

As you see yourself, in this frame of reference the equations are much more complicated because if the time dependence of J.


If you're familiar with Lagrangian and Hamiltonian mechanics I'd suggest to try from the beginning once again, as the concept there is much more profound and easier applicable. (you could use phi, theta and r as independent generalised coordinates, since you have 2-dimensional translation and 1-dimensional rotation). In this case you could also admit gravitational field or any other non-dissipative force and still obtain the correct equations of motion. Furthermore, the integrals of motion are directly to read out of the Lagrangian.

 

[kof9595995]

You have to always be careful with the choice of frame of reference. Observe that the torque equals the time derivative of the entire angular momentum. As your calculations are absolutely correct, it follows:

$$M=\dot L=\frac{d}{dt}(J\dot\theta)=\dot J\dot\theta+J\ddot\theta=\frac{d}{dt}(\frac{1}{12}ml^2+m(x(t)+y(t)))\dot\theta+J\ddot\theta\neq J\ddot\theta$$

so the 3rd. equation does not hold any more.

Yes, that's really a big mistake. Thanks for the corection

I would suggest to choose the axis of rotation in the centre of mass, so that you obtain a simple equation for theta (you won't need the parallel axis thm. )

Well, then that would be a non-inertial frame, I've thought about this, but I finally couldn't figure out how to apply a pseudo force on it so I gave up the attempt .

If you're familiar with Lagrangian and Hamiltonian mechanics I'd suggest to try from the beginning once again, as the concept there is much more profound and easier applicable. (you could use phi, theta and r as independent generalised coordinates, since you have 2-dimensional translation and 1-dimensional rotation). In this case you could also admit gravitational field or any other non-dissipative force and still obtain the correct equations of motion. Furthermore, the integrals of motion are directly to read out of the Lagrangian.

I will learn these stuff this semester and I'll try the method later.
Anyway the equation still seems to be coupled, so I guess it can't even be uncoupled? And let's generalised the question, how can I know if the equation can't be uncoupled?By failing infinitely many times?

 

[kof9595995]

then, it follows for the torque using the first two equations:
$$M = F(x\cos\theta-y\sin\theta-l/2)=F(m/Fx\ddot y-m/Fy\ddot x-l/2)=m(x\ddot y+\dot x\dot y-\dot y\dot x-y\ddot x)=m\frac{d}{dt}(x\dot y-y\dot x)$$

Well, maybe I'm just too new to ODE stuff, I really appreciate this graceful step.Seems that you constructed a derivetive of a Wronskian, it just never occurred to me before. But you probably missed the l/2 term.

 

[Marin]

yes, that's correct. I did miss the l/2 term ;)

As to the Wronskain, it was't meant that way, but if there's such a method it's fine. What I tried to do is to add and subtract certain term, so that the derivative becomes explicit. By doing so sometimes one approaches a direct integration of the equation (but this didn't entirely happen here).

As to the decoupling problem:

As far as I know, you can't say anything in general about nonlinear ODEs or ODE-systems. Non-linearity is handled mostly by doing the correct coordinate transformation (which has to be guessed, that's why it's very difficult). Another, more common way to handle it is to linearise your system by Taylor expansions of every non-linearity. This will produce the solutions for small angles theta and phi. (one mostly common non-linear ODE system is the Lotka-Volterra prey-predator model, I recommend on getting familiar with it)

Thus, if the system is linear, then rewrite it in matrix-vector notation. There are 2 possibilities:

1) matrix can be diagonalised, then it's all clear (just look at the algorithm, you will need the eigenvalue and eigenvetor theory)
2) matrix cannot be diagonalised - cf. 'Jordan normal form, matrix exponentials and s.o.)

Nevertheless, there are some harsh theorems of linear algebra (existence and uniqueness of the Jordan normal form) that say that linear systems can always be decoupled. Whether this could be done analytically is another topic.


Non-inertial frames:

Once you've done analytical mechanics, you'll no longer be afraid of the nonlinear systems, since every pseudo force will be contained in the coordinate transformation, if you do it correctly.

Here's an interesting course about ODEs: http://www.youtube.com/results?sear...al+equations&search_type=&aq=0&oq=mit+differe

It's not strictly mathematical, but it's sufficient for the needs of physics.

 

[kof9595995]

Thanks, your replies are really helpful.