chriswall89@hotmail.
- 9
- 0
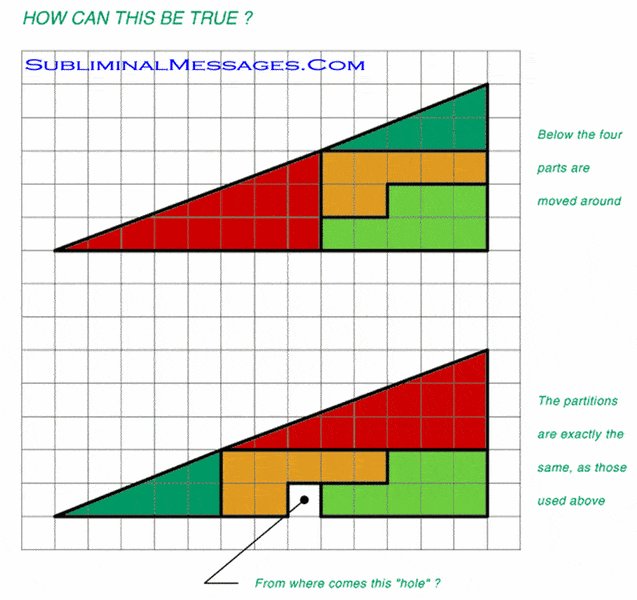
Ok, I've just signed up to this forum and i see there are a lot of very smart people and i just wondered if anyone knows the answer to the mensa triangle problem. I've sat and stared at it for hours and still i have no answer. Any theories.