earthloop
- 25
- 0
Hi Everyone.
Just a brief hello before the problem! I am a new user as of today. I am studying Electrical Engineering in my spare time after work, and currently working full time an electronics service engineer. I have tried to make the problem as clear as I can, any help would be highly appreciated.
The problem asks to produce a current via two methods. I have obtained two answers that are different and would like to know where I went wrong.
For the record, most of my calculations were done within matlab. This is also my first attempt at using matrices, so I am unsure if my calculations were correct (or whether it was necessary to use matrices in the first place).
Determine the current I by
A) Mesh Analysis
B) Nodal Analysis
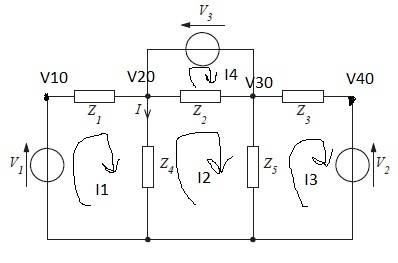
<br /> \begin{align}<br /> &v1 = 120 < 0° V\\<br /> &v2 = 120 < 90° V\\<br /> &v3 = 20 < 45° V\\<br /> &z1 = 2 Ω\\<br /> &z2 = –j5 Ω\\<br /> &z3 = 4 Ω\\<br /> &z4 = –j5 Ω\\<br /> &z5 = j4 Ω\\<br /> \\<br /> &Node Voltages\\<br /> &V10\\<br /> &V20\\<br /> &V30\\<br /> &V40\\<br /> \\<br /> &Mesh Loops\\<br /> &I1\\<br /> &I2\\<br /> &I3\\<br /> &I4\\<br /> \end{align}<br />
A)[/B]
I1 -
v1-I1(z1+z4)+I2(z4) = 0
I1(-2+j5)+I2(-j5) = -120
I2 -
I1(z4)-I2(z2+z4+z5)+I3(z5)+I4(z2) = 0
I1(-j5)+I2(j6)+I3(j4)+I4(-j5) = 0
I3 -
I2(z5)-I3(z3+z5)-v2
I2(j4)+I3(-4-j4) = j120
I4 -
I2(z2)-I4(z2)-v3
I2(-j5)+I4(j5) = 14.14+ j 14.14
Matrix A
\begin{pmatrix}<br /> -2+j5 & -j5 & 0 & 0\\<br /> -j5 & j6 & j4 & -j5\\<br /> 0 & j4 & -4-j4 & 0\\<br /> 0 & -j5 & 0 & j5\\<br /> \end{pmatrix}<br />
Matrix B
\begin{pmatrix}<br /> -120\\<br /> 0\\<br /> j120\\<br /> 14.14+j14.14\\<br /> \end{pmatrix}<br />
<br /> INV(A)*B = C<br />
Matrix C - from matlab
\begin{pmatrix}<br /> 16.8112 - j22.8793\\<br /> 25.9629 - j40.1548\\<br /> 18.0588 - j22.0959\\<br /> 28.7914 - j42.9832\\<br /> \end{pmatrix}<br />
I = I1-I2-I4
I = 16.8112 - j22.8793 - 25.9629 - j40.1548 - 28.7914 - j42.9832
I = -37.9431 + j60.2587 A
B)
V20 - V30 = V3
Node 2+3 supernode
\frac{v1-V20}{z1} - \frac{V20}{z4} - \frac{V30}{z5} + \frac{v2-V30}{z3} = 0
X = V20(-0.5 - j0.5) + V30(-0.25+j0.25) = -60-j30
(V20-V30 = v3) * (-0.25+j0.25)
Y = V20(-0.25+j0.25) + V30(0.25-j0.25) = -5\sqrt{2}
Add X + Y
V20(-0.75+j0.05) = 67.07-j30
V20 = \frac{-67.07-j30}{-0.75+j0.05}
V20 = 86.37 + 45.76 V
I = \frac{V20}{z4} = -9.15 +j17.27
As you can see I have very different answers, and have scratched my head all weekend over it.
Any help would be appreciated.
Thanks!
Earthloop
Just a brief hello before the problem! I am a new user as of today. I am studying Electrical Engineering in my spare time after work, and currently working full time an electronics service engineer. I have tried to make the problem as clear as I can, any help would be highly appreciated.
The problem asks to produce a current via two methods. I have obtained two answers that are different and would like to know where I went wrong.
For the record, most of my calculations were done within matlab. This is also my first attempt at using matrices, so I am unsure if my calculations were correct (or whether it was necessary to use matrices in the first place).
Homework Statement
Determine the current I by
A) Mesh Analysis
B) Nodal Analysis
<br /> \begin{align}<br /> &v1 = 120 < 0° V\\<br /> &v2 = 120 < 90° V\\<br /> &v3 = 20 < 45° V\\<br /> &z1 = 2 Ω\\<br /> &z2 = –j5 Ω\\<br /> &z3 = 4 Ω\\<br /> &z4 = –j5 Ω\\<br /> &z5 = j4 Ω\\<br /> \\<br /> &Node Voltages\\<br /> &V10\\<br /> &V20\\<br /> &V30\\<br /> &V40\\<br /> \\<br /> &Mesh Loops\\<br /> &I1\\<br /> &I2\\<br /> &I3\\<br /> &I4\\<br /> \end{align}<br />
Homework Equations
The Attempt at a Solution
A)[/B]
I1 -
v1-I1(z1+z4)+I2(z4) = 0
I1(-2+j5)+I2(-j5) = -120
I2 -
I1(z4)-I2(z2+z4+z5)+I3(z5)+I4(z2) = 0
I1(-j5)+I2(j6)+I3(j4)+I4(-j5) = 0
I3 -
I2(z5)-I3(z3+z5)-v2
I2(j4)+I3(-4-j4) = j120
I4 -
I2(z2)-I4(z2)-v3
I2(-j5)+I4(j5) = 14.14+ j 14.14
Matrix A
\begin{pmatrix}<br /> -2+j5 & -j5 & 0 & 0\\<br /> -j5 & j6 & j4 & -j5\\<br /> 0 & j4 & -4-j4 & 0\\<br /> 0 & -j5 & 0 & j5\\<br /> \end{pmatrix}<br />
Matrix B
\begin{pmatrix}<br /> -120\\<br /> 0\\<br /> j120\\<br /> 14.14+j14.14\\<br /> \end{pmatrix}<br />
<br /> INV(A)*B = C<br />
Matrix C - from matlab
\begin{pmatrix}<br /> 16.8112 - j22.8793\\<br /> 25.9629 - j40.1548\\<br /> 18.0588 - j22.0959\\<br /> 28.7914 - j42.9832\\<br /> \end{pmatrix}<br />
I = I1-I2-I4
I = 16.8112 - j22.8793 - 25.9629 - j40.1548 - 28.7914 - j42.9832
I = -37.9431 + j60.2587 A
B)
V20 - V30 = V3
Node 2+3 supernode
\frac{v1-V20}{z1} - \frac{V20}{z4} - \frac{V30}{z5} + \frac{v2-V30}{z3} = 0
X = V20(-0.5 - j0.5) + V30(-0.25+j0.25) = -60-j30
(V20-V30 = v3) * (-0.25+j0.25)
Y = V20(-0.25+j0.25) + V30(0.25-j0.25) = -5\sqrt{2}
Add X + Y
V20(-0.75+j0.05) = 67.07-j30
V20 = \frac{-67.07-j30}{-0.75+j0.05}
V20 = 86.37 + 45.76 V
I = \frac{V20}{z4} = -9.15 +j17.27
As you can see I have very different answers, and have scratched my head all weekend over it.
Any help would be appreciated.
Thanks!
Earthloop