Solve this Circuit using both Nodal Analysis and Mesh Analysis

[pgetts]

Homework Statement

[/B]
Determine, Using the values given in TABLE A, the current I in the circuit of figure 2 by
(a) Mesh analysis
(b) Nodal analysis

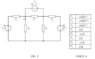
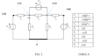
Circuit diagram and given variable attached.
V1 = 120
V2 = j120
V3 = 14.142+j14.142
Z1= 2
Z2=-J5
Z3=4
Z4=-J5
Z5=J4

Homework Equations

[/B]
KVL
KCL
Ohms law
Supernode

The Attempt at a Solution

[/B]
(a) complete, answer (-9.2+j17.2)

(b)

Ref node 0 on bottom line of diagram.
Node V10 between V1 and Z1 = 120V
Node V40 between V2 and Z3 = j120
Node V20 between V3, Z4 and Z1
Node V30 between V3, Z5 and Z3.

Replace V30 with super node. V20-V3)

(V1-V20/Z1)+(0-V20/Z4)+(-(V20-V3/Z5)+(V2-(V20-V3/Z3)=0

(V1-V20/Z1) - (V20/Z4) + (V3-V20/Z5) + (V2-V20+V3/Z3) = 0

-V20(1/Z1+1/Z4+1/Z5+1/Z3) + (V1*1/Z1) + (V2*1/Z3) + (V3*1/Z3) + (V3*1/Z5) = 0

-V20((1/2)+(1/-j5)+(1/j4)+(1/4) + (120*(1/2)+(V2*1/4)+(14.142+j14.142*1/4)+(14.142+j14.142*1/j4)=0

-V20(0.75+j0.05) + (60+j37.071)=0

(60+j37.071)=V20(0.75+j0.05)

V20 = (60+j37.071)/(0.75+j0.05)

V20 = (82.9266 +j43.8996)

V20/Z4 = I

i =-8.77992 +j16.5853. Which is off from my mesh answer. working backwards i expected due to the current from the mesh answer, times Z4 to be looking for a V20 voltage of (86+j46) can anyone help. Thanks in advance.

 

[magoo]

In your first equation, did you mean:

V1-V20/Z1

or
(V1-V20)/Z1

 

[pgetts]

V1-V20/Z1

 

[magoo]

If you are using nodal analysis, the current is given by the quantity - difference in node voltages - divided by the impedance between them. You need to revisit this.

 

[pgetts]

Thanks Magoo it's really appreciated as I've been struggling with this for weeks though I'm still not following. As my V20 is connected via the reference node the difference in quantity would be 0-V20 no? or am I missing the point that node V20 would be V1-V20. If you could point me in the direction of any additional reading material it would be a massive help as the college notes for the whole course I'm on are, being polite, less than useless.

 

[magoo]

I redrew your circuit below.

With the reference node 0, there is no need to introduce V20 and V40. V20 is simply V1 and V40 is V2.

Let's say you have two nodes, Vhere and Vthere. Start at Vhere.

The term, (Vhere - Vthere)/Z, will represent a current in the direction of Vthere.

In your actual case, there will be a few "Vthere" terms, but the procedure is still the same.

See if any of this helps.

I don't have any references to suggest. Why not do a search on nodal equations for circuit analysis or something like that.

 

[magoo]

This link has some examples that might help.

http://mathonweb.com/help/backgd5.htm

 

[The Electrician]

I redrew your circuit below.

View attachment 230649

The OP described the designators he is using in post #1:

"Ref node 0 on bottom line of diagram.
Node V10 between V1 and Z1 = 120V
Node V40 between V2 and Z3 = j120
Node V20 between V3, Z4 and Z1
Node V30 between V3, Z5 and Z3."

Your diagram is different.

 

[magoo]

Yes, you are correct. The point is you still don't need to introduce V10 and V40. They are V1 and V2, respectively.

 

[The Electrician]

Yes, you are correct. The point is you still don't need to introduce V10 and V40. They are V1 and V2, respectively.

True enough, and the OP didn't use V10 and V40 in his equations, but you showed two different nodes both labeled V20, which he does use.

 

[magoo]

Ok, here is a corrected drawing.

My suggestion to the OP would be to write the nodal equations for node V20 and for node V30 based on the methodology that I outlined.

 

[pgetts]

Thanks guys.

So reference node is defined at the bottom.

Trivial Nodes would be V10 & V40 as they are actually just V1 and V2 respective

So my super node is defined as V20-V30=V3.

My currents assumption will be all leaving the supernode so I will get the equation.

V20-V1/Z1+V20/Z4+V30/Z5+V30-V2/Z3=0

-V1/Z1+V20(1/Z1+1/Z4)+V30(1/Z5+1/Z3+-V2/Z3=0

Correct method so far?

 

[magoo]

Rather than work with a supernode involving V20, V30 and V3, I would suggest sticking with nodal equations for a single node like V20 or V30.

The nodal equations must take into account Vhere and Vthere to do it correctly.

Your V20 - V1/Z1 should be (V20 - V1)/Z1. This procedure follows for the other currents as well.

 

[The Electrician]

Thanks guys.

So reference node is defined at the bottom.

Trivial Nodes would be V10 & V40 as they are actually just V1 and V2 respective

So my super node is defined as V20-V30=V3.

My currents assumption will be all leaving the supernode so I will get the equation.

V20-V1/Z1+V20/Z4+V30/Z5+V30-V2/Z3=0

-V1/Z1+V20(1/Z1+1/Z4)+V30(1/Z5+1/Z3+-V2/Z3=0

Correct method so far?

Substitute (V20 - V3) for V30, plug in numerical values for everything, and you're good to go.

 

[pgetts]

Ah thanks fellas. Finally got the same result as my Mesh analysis. Thanks again.

 

[magoo]

Glad to hear that.