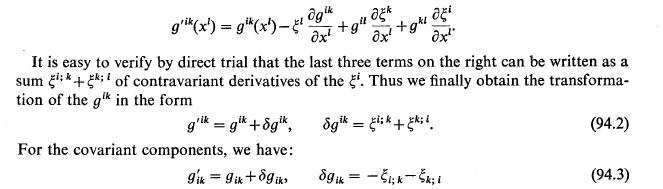I Metric transformation under coordinate transformation

[Tursinbay]

In the second volume, Field Theory, of popular series of Theoretical Physics by Landau-Lifschitz are given following equations as in attached file from the book. Here is considered metric change under coordinate transformation. How is the new, prime metric expressed in original coordinates is obtained as in (94.2). In right hand side of the equation right before (94.2) the last three terms is equal to Killing equations as it is said that could be verified by direct trial. What would direct trial like. I checked but got different results.

 

[strangerep]

[...] I checked but got different results.

But you did not show us your attempt here, so how can anyone see what you might have done wrong?

Btw, here is a Latex introduction to help you get started with using Latex to display math here on PF.

 

[haushofer]

We don't have paranormal powers here at PF :P

 

[pervect]

Direct trial would just (IMO) be evaluating
$$\xi^{i;k}+\xi^{k;l}$$

To do this I'd write $$\xi^{i;k} = g^{kp} \, \xi^i{}_{;p} \approx \eta^{kp} \, \xi^i{}_{;p} = \eta^{kp} \nabla_p \xi^i$$

and carry on from there, rewriting the other term in the same manner, and using the Christoffel symbols to calculate the covariant derivative $\nabla_p \xi^i$. There's probably a way to write this more clearly without switching out of the semi-colon notation midstream, but I never liked the semicolon notation that much, hopefully you can deal with the notation switch.

I haven't actually carried this plan out. The "approximation" here is a standard one: raising (or lowering, if applicable, which it isn't in this case) indices with the unperturbed flat metric $\eta^{ij}$ rather than the full metric $g^{ij} = \eta^{ij} + h^{ij}$. This works in linear theory because we're only keeping terms of the first order.

I'm too lazy to carry this out in full, but that's the approach I'd use if I wasn't too lazy.

 

[Tursinbay]

But it is not mentioned that metric is almost flat. I carrried out these calculations. it seems everything is correct. I am missing key point here.

 

[strangerep]

You're just missing an index manipulation trick. In the final term, swap the $m$ and $n$ dummy indices. You'll find that the 2nd and 3rd terms in your first parentheses cancel.

(If you make the effort of writing out your last line properly in latex, I'll make the effort of showing you the manipulation in more detail, also in latex.)

 

[Tursinbay]

Here is the last line

$$\frac 1 2 \left( \frac {\partial g_{nm}} {\partial x^l} + \frac {\partial g_{nl}} {\partial x^m} - \frac {\partial g_{lm}} {\partial x^n} \right) \xi^l \left(g^{mk}g^{in}+g^{mi}g^{kn} \right)$$

 

[samalkhaiat]

In the second volume, Field Theory, of popular series of Theoretical Physics by Landau-Lifschitz are given following equations as in attached file from the book. Here is considered metric change under coordinate transformation. How is the new, prime metric expressed in original coordinates is obtained as in (94.2). In right hand side of the equation right before (94.2) the last three terms is equal to Killing equations as it is said that could be verified by direct trial. What would direct trial like. I checked but got different results.

Use the metricity condition \nabla_{l}g^{ik} = 0 to express -\partial_{l}g^{ik} = g^{in}\ \Gamma^{k}_{ln} + g^{nk} \ \Gamma^{i}_{ln} . Substitute the above in the first term of the expression bellow \delta g^{ik} = - \epsilon^{l}\partial_{l}g^{ik} +g^{in}\partial_{n}\epsilon^{k} + g^{nk}\partial_{n}\epsilon^{i} . You will then see that the first term and the third term add up to g^{in}\nabla_{n}\epsilon^{k} \equiv \nabla^{i}\epsilon^{k}, while the second and the fourth terms give you g^{nk}\nabla_{n}\epsilon^{i} \equiv \nabla^{k}\epsilon^{i}.

Of course you obtain the same result, if you substitute \partial \epsilon = \nabla \epsilon - \epsilon \Gamma in the last two terms of \delta g = - \epsilon \cdot \partial g + g \cdot \partial \epsilon + g \cdot \partial \epsilon , and then collect the \Gamma’s terms to form \nabla g: \delta g = - \epsilon \cdot \nabla g + g \cdot \nabla \epsilon + g \cdot \nabla \epsilon . So, the metricity condition \nabla g = 0 implies and is implied by \delta g^{ik} = \nabla^{i} \epsilon^{k} + \nabla^{k}\epsilon^{i}.

 

[strangerep]

Here is the last line$$\frac 1 2 \left( \frac {\partial g_{nm}} {\partial x^l} + \frac {\partial g_{nl}} {\partial x^m} - \frac {\partial g_{lm}} {\partial x^n} \right) \xi^l \left(g^{mk}g^{in}+g^{mi}g^{kn} \right)$$

OK, so let's concentrate on just this subexpression:
$$\left( \frac {\partial g_{nm}} {\partial x^l} + \frac {\partial g_{nl}} {\partial x^m} - \frac {\partial g_{lm}} {\partial x^n} \right) g^{mk}g^{in}~~~~~~~~ (1) $$ The $m$ and $n$ indices are dummy summation indices, so we may interchange them throughout, i.e., $$\left( \frac {\partial g_{mn}} {\partial x^l} + \frac {\partial g_{ml}} {\partial x^n} - \frac {\partial g_{ln}} {\partial x^m} \right) g^{nk}g^{im} ~~~~~~~~ (2)$$ Then, since $g$ is a symmetric tensor, this can be rewritten as $$\left( \frac {\partial g_{nm}} {\partial x^l} + \frac {\partial g_{lm}} {\partial x^n} - \frac {\partial g_{nl}} {\partial x^m} \right) g^{mi}g^{kn}~~~~~~~~ (3)$$ Notice how, if you swap $k,i$ in (3), then add it to (1), the 2nd and 3rd terms in the parentheses cancel? That's the step you were missing in the last line of your post #5.

Actually, there are some shortcut techniques that would help you perform such computations faster.

a) If you have an expression like $A_{ij} S^{ij}$, where $A$ is antisymmetric and $S$ is symmetric, then the expression is 0.

b) Instead of writing out each expression tediously as you did in post #5, you could have just done it for $\xi^{k;i}$ and then swapped the $k,i$ indices at the end to get the 2nd term.

c) Because the 2nd parenthesis factor is symmetric in $k,i$ (after swapping the $m,n$ dummy indices in the 2nd term), you can immediately know that any term inside the 1st parentheses which is antisymmetric in $m,n$ will not contribute, because of point (a) above.

I hope that helps.

(Btw, be sure to study Samalkhaiat's post #8 carefully. Sometimes it takes several readings and a bit of pen+paper work to get full value from his posts.)

 

[Tursinbay]

Dear Samalkhaiat and Strangerep,

your comments are very helpful. Using the metricity condition and symmetries I obtained the wished result. I appreiciate your comments!