Metronome question: Figuring out net torque and expression for beats per minute?

[nukeman]

Homework Statement

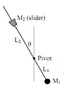
A metronome is a device used by musicians to help them adjust
the timing of their music to a standard number of beats per
minute. The position of the moveable slider determines the
frequency. It is possible to build a simple mechanical
metronome using a light stick and two masses, as shown in the
diagram.

(a) Assume the metronome is displaced from the vertical by an
angle, theta, as shown in the figure. Find an expression for the net
torque on the metronome about the pivot. Go through the
necessary steps to show that it will oscillate in SHM providing 
is a small angle and M1L1 > M2L2. Find an expression for the
number of beats per second of the metronome (note that there
are 2 beats per cycle of oscillation).

(b) Suppose M1 = 0.200 kg, M2 = 0.0500 kg, and L1 = 5.0 cm. Calculate the number of
beats per minute if:
(i) L2 = 16.3 cm. (Check your answer: 60 beats per minute.)
(ii) L2 = 6.8 cm.

Here is the image for the problem question I am having: http://i43.tinypic.com/sgiwb5.png

Homework Equations

The Attempt at a Solution

Really need help with this:

The torque on M1 is –(M1 *g * L1 *sin(theta)) correct? The torque on M2 is positive (CCW). I add them together to get net torque right?

How do I add them together?

Also after that, how do I find an expression for the numbe of beats per second, as stated in the question.

 

[SammyS]

Here is the image for anybody reading this thread.

 

[nukeman]

Thanks sammy!

Any help on this would be great! Having some issues :(

 

[nukeman]

Anyone? :)

 

[nukeman]

is this correct?

The mechanism is a physical pendulum. f = (1/2π)√[m*g*L/I] where m = M1+M2, L = distance from CM to pivot, and I = moment of inertia about pivot.
Ergo, beat frequency fb = f/2 = (1/4π)√[mgL/I]