- #1
- 22,183
- 3,321
Summer, July, hot weather: every reason is good enough for some new challenge questions.
NEW: ranking can be found here: https://www.physicsforums.com/threads/micromass-big-challenge-ranking.879070/
For high school and first year university students, there is a special challenge thread for you! https://www.physicsforums.com/threads/micromass-big-high-school-challenge-thread.879086/
RULES:
1. In a village of ##2016## people, prove that the probability that exactly ##m## days (ignore leap years) are not a birthday can be approximated by a Poisson distribution.
2. SOLVED BY Charles Link, Infrared Consider the spiral in the following graphic. The spiral is started with an isosceles right triangle with rectangular sides ##1##. At every step, we form adjoin a new triangle having one rectangular leg the hypothenuse of the previous triangle and the other leg equal to 1.

We see that after we add 17 triangles, we have approximately performed one rotation. Let ##K## be the number of rotations that are performed after adding a googol (i.e.\ ##10^{100}##) triangles. Without using a calculator, find the first digit of ##K## and the number of digits of ##K##. This answer may use approximation techniques if they are shown to be valid.
3. SOLVED BY Infrared Compute for for each ##x\in \mathbb{R}##
[tex]\lim_{n\rightarrow +\infty} \lim_{m\rightarrow +\infty} |\cos(n! \pi x)|^m[/tex]
4. a) SOLVED BY QuantumQuest In the Pascal triangle, replace all odd numbers by a black dot and remove all even numbers. For example, the first three rows of the Pascal triangle are
[tex]\begin{array}{|ccccc|}
\hline
& & 1 & & \\
& 1 & & 1 & \\
1 & & 2 & & 1\\
\hline
\end{array}
[/tex]
is transformed to
[tex]\begin{array}{|ccccc|}
\hline
& & \bullet & & \\
& \bullet & & \bullet & \\
\bullet & & & & \bullet\\
\hline
\end{array}
[/tex]
State and prove a conjecture relating the resulting figure to the Sierpinski triangle.
4. b) SOLVED BY Math_QED Let ##s_n## be the product of the terms in the ##n##th row of the Pascal triangle. Find
[tex]\lim_{n\rightarrow +\infty} \frac{s_{n-1}s_{n+1}}{s_n^2}[/tex]
5. SOLVED BY QuantumQuest A drunk man is walking on an infinite grid ##\mathbb{Z}\times \mathbb{Z}##. Every time he gets to a point on the grid, he chooses at random between the directions "up", "down", "left", "right" so that each direction has equal probability. After choosing a direction, he continues in that direction until the next grid point. The drunk man starts at the pub which is located at ##(0,0)## and wishes to get home which is located at ##(10,10)##. Show that the drunk man will eventually reach his home with probability ##1##.
6. SOLVED BY Erland Show that every point in ##[-1,1]## is an accumulation point of the sequence ##x_n = \sin n ##.
7. SOLVED BY Svein Dana is moving into a mansion, and she needs a huge whiteboard. This whiteboard is to be so heavy that it cannot be lifted; only wheeled. A certain corridor is 2.7 metres wide, and is perpendicular to a 6.4 metre wide corridor. What is the length (in metres) of the longest whiteboard that she can manoeuvre around the corner?
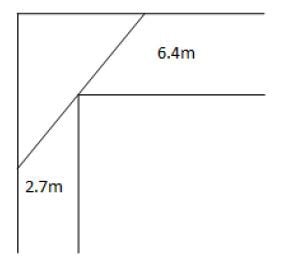
8. Let ##G## be a finite group and let ##p## be the smallest prime number which divide ##|G|##. Prove that every subgroup ##H## of ##G## such that ##p|H| = |G|## is normal. Use this to find all groups of order ##pq## with ##p## and ##q## (not necessarily distinct) primes.
9. SOLVED BY Infrared Let ##G## a semigroup (a set with an associative multiplicaton). Prove that the following three conditions are equivalent:
a) ##G## is a group
b) ##G## is not empty and for all ##a## and ##b## in ##G##, we have that the equation ##ax=b## has a solution and ##xa = b## has a solution.
c) There exists an ##e \in G## such that ##xe = x## for all ##x\in G##. Furthermore, for that specific ##e##, we have that for any ##x\in G##, there is some ##x'\in G## such that ##xx' = e##.
10. SOLVED BY mfb Let ##X## be a set equipped with two operations ##\times## and ##*##. Suppose that
a) There is an ##e\in X## such that for each ##x\in X## we have ##e*x = x*e = x##.
b) There is an ##e'\in X## such that for each ##x\in X## we have ##e'\times x = x\times e' = x##.
c) for all ##a,b,c,d\in X## we have ##(a\times b)*(c\times d) = (a*c) \times (b*d)##.
Prove that ##\times## and ##*## are the same. Prove furthermore, that these operations are commutative, associative and have ##e=e'##.
NEW: ranking can be found here: https://www.physicsforums.com/threads/micromass-big-challenge-ranking.879070/
For high school and first year university students, there is a special challenge thread for you! https://www.physicsforums.com/threads/micromass-big-high-school-challenge-thread.879086/
RULES:
- In order for a solution to count, a full derivation or proof must be given. Answers with no proof will be ignored.
- It is fine to use nontrivial results without proof as long as you cite them and as long as it is "common knowledge to all mathematicians". Whether the latter is satisfied will be decided on a case-by-case basis.
- If you have seen the problem before and remember the solution, you cannot participate in the solution to that problem.
- You are allowed to use google, wolframalpha or any other resource. However, you are not allowed to search the question directly. So if the question was to solve an integral, you are allowed to obtain numerical answers from software, you are allowed to search for useful integration techniques, but you cannot type in the integral in wolframalpha to see its solution.
1. In a village of ##2016## people, prove that the probability that exactly ##m## days (ignore leap years) are not a birthday can be approximated by a Poisson distribution.
2. SOLVED BY Charles Link, Infrared Consider the spiral in the following graphic. The spiral is started with an isosceles right triangle with rectangular sides ##1##. At every step, we form adjoin a new triangle having one rectangular leg the hypothenuse of the previous triangle and the other leg equal to 1.
We see that after we add 17 triangles, we have approximately performed one rotation. Let ##K## be the number of rotations that are performed after adding a googol (i.e.\ ##10^{100}##) triangles. Without using a calculator, find the first digit of ##K## and the number of digits of ##K##. This answer may use approximation techniques if they are shown to be valid.
3. SOLVED BY Infrared Compute for for each ##x\in \mathbb{R}##
[tex]\lim_{n\rightarrow +\infty} \lim_{m\rightarrow +\infty} |\cos(n! \pi x)|^m[/tex]
4. a) SOLVED BY QuantumQuest In the Pascal triangle, replace all odd numbers by a black dot and remove all even numbers. For example, the first three rows of the Pascal triangle are
[tex]\begin{array}{|ccccc|}
\hline
& & 1 & & \\
& 1 & & 1 & \\
1 & & 2 & & 1\\
\hline
\end{array}
[/tex]
is transformed to
[tex]\begin{array}{|ccccc|}
\hline
& & \bullet & & \\
& \bullet & & \bullet & \\
\bullet & & & & \bullet\\
\hline
\end{array}
[/tex]
State and prove a conjecture relating the resulting figure to the Sierpinski triangle.
4. b) SOLVED BY Math_QED Let ##s_n## be the product of the terms in the ##n##th row of the Pascal triangle. Find
[tex]\lim_{n\rightarrow +\infty} \frac{s_{n-1}s_{n+1}}{s_n^2}[/tex]
5. SOLVED BY QuantumQuest A drunk man is walking on an infinite grid ##\mathbb{Z}\times \mathbb{Z}##. Every time he gets to a point on the grid, he chooses at random between the directions "up", "down", "left", "right" so that each direction has equal probability. After choosing a direction, he continues in that direction until the next grid point. The drunk man starts at the pub which is located at ##(0,0)## and wishes to get home which is located at ##(10,10)##. Show that the drunk man will eventually reach his home with probability ##1##.
6. SOLVED BY Erland Show that every point in ##[-1,1]## is an accumulation point of the sequence ##x_n = \sin n ##.
7. SOLVED BY Svein Dana is moving into a mansion, and she needs a huge whiteboard. This whiteboard is to be so heavy that it cannot be lifted; only wheeled. A certain corridor is 2.7 metres wide, and is perpendicular to a 6.4 metre wide corridor. What is the length (in metres) of the longest whiteboard that she can manoeuvre around the corner?
8. Let ##G## be a finite group and let ##p## be the smallest prime number which divide ##|G|##. Prove that every subgroup ##H## of ##G## such that ##p|H| = |G|## is normal. Use this to find all groups of order ##pq## with ##p## and ##q## (not necessarily distinct) primes.
9. SOLVED BY Infrared Let ##G## a semigroup (a set with an associative multiplicaton). Prove that the following three conditions are equivalent:
a) ##G## is a group
b) ##G## is not empty and for all ##a## and ##b## in ##G##, we have that the equation ##ax=b## has a solution and ##xa = b## has a solution.
c) There exists an ##e \in G## such that ##xe = x## for all ##x\in G##. Furthermore, for that specific ##e##, we have that for any ##x\in G##, there is some ##x'\in G## such that ##xx' = e##.
10. SOLVED BY mfb Let ##X## be a set equipped with two operations ##\times## and ##*##. Suppose that
a) There is an ##e\in X## such that for each ##x\in X## we have ##e*x = x*e = x##.
b) There is an ##e'\in X## such that for each ##x\in X## we have ##e'\times x = x\times e' = x##.
c) for all ##a,b,c,d\in X## we have ##(a\times b)*(c\times d) = (a*c) \times (b*d)##.
Prove that ##\times## and ##*## are the same. Prove furthermore, that these operations are commutative, associative and have ##e=e'##.
Last edited: