Minimum force required to form sphere

[Tanya Sharma]

Homework Statement

Homework Equations

The Attempt at a Solution

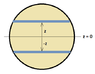
Doing a vertical force balance 2Fcosθ=mg ,where m is the mass of water .

Not sure how to proceed .

What role does the pin hole at the top play ?

I would be grateful if somebody could help me with the problem.

 

[Simon Bridge]

What role does the pin hole at the top play ?

... that is the key question.
Think about it - what does putting a pinhole in the top do that not having a hole there not do?
i.e. imagine there is also a pinhole at the bottom - what difference would a hole at the top make?

 

[haruspex]

Pace Simon, but the pinhole at the top is only to get around a complication that the setter did not want to get tangled up with. It looks like you didn't notice the complication anyway, so what you have done so far is ok. But you need another equation. The answer to the question should be an actual number, not dependent on any variables.

 

[Chestermiller]

Here's a hint Tanya: Think hydrostatic.

Chet

 

[Tanya Sharma]

I have thought about it . Please elaborate .

 

[Chestermiller]

I have thought about it . Please elaborate .

The pressure (force per unit area) on each hemisphere is going to increase with depth. To get the horizontal force on each hemisphere, you need to integrate. I haven't figured out yet whether you also need to do a moments balance.

Chet

 

[Tanya Sharma]

Chet ,

I somehow feel there is a simpler , less mathematically rigorous solution to this problem .

Is the force across the interface between the spheres given by $$2 ρg\int_0^R \sqrt{R^2 - (R-h)^2}h dh$$ ? But then ρ comes in picture and the integral also doesn't look nice .

 

[TSny]

Is the force across the interface between the spheres given by $$2 ρg\int_0^R \sqrt{R^2 - (R-h)^2}h dh$$ ? But then ρ comes in picture and the integral also doesn't look nice .

The integrand looks good. Check the limits.

If you want to avoid the integration, consider a vertically oriented circular area submerged in a static fluid. Consider two, symmetrically placed horizontal strips of area as shown in blue. How do the pressures at each of these strips compare to the pressure at z = 0? Does the sum of the forces on the two strips simplify?

 

[Tanya Sharma]

The integrand looks good. But your limits don't seem right.

It should be from 0 to 2R . Right?

If you want to avoid the integration,

Yes .

consider a vertically oriented circular area submerged in a static fluid. Consider two, symmetrically placed horizontal strips of area as shown in blue. How do the pressures at each of these strips compare to the pressure at z = 0?

If we denote the pressure at z=0 to be P ,pressure at the upper blue strip is P-ρgz . Pressure at the lower blue strip is P+ρgz

Does the sum of the forces on the two strips simplify?

2P . Is that so ?

Edit : 2P is sum of pressures .

 

[TSny]

It should be from 0 to 2R . Right?

Yes.

If we denote the pressure at z=0 to be P ,pressure at the upper blue strip is P-ρgz . Pressure at the lower blue strip is P+ρgz

Yes.

2P . Is that so ?

This is the total force on the two strips?

 

[Tanya Sharma]

Total force on two strips is 4P$\sqrt{R^2-z^2}dz$ .

 

[TSny]

Yikes. (Correct, but messy.) Let the area of both strips together be ΔA. Express the sum of the forces on the two strips in terms of P and ΔA.

 

[Tanya Sharma]

2PΔA

 

[TSny]

2PΔA

Well, I was taking ΔA as representing the sum of the areas of the two strips. If so, then your expression is not quite corrrect.

 

[Tanya Sharma]

Total force on vertically oriented circular area should be $\pi ρgR^3$ . Is that correct ?

 

[TSny]

Total force on the circular strip should be $\pi ρgR^3$ . Is that correct ?

Should atmospheric pressure be included?

 

[Tanya Sharma]

It should be $(P_{atm}+ρgR)πR^2$ ?

 

[TSny]

Yes, the total force on the circle is the pressure at the center times the total area of the circle. Do you see why they put the little hole at the top?

 

[Tanya Sharma]

What should be the next step ?

 

[TSny]

The next step should probably be to take a break and sleep on it. (Isn't it late there?)

Anyway, one thing to think about is how your result for the circle can be used to get the net horizontal force of the fluid on the inner surface of the hemisphere. Also think about the effect of external atmospheric pressure acting on the outer curved surface of the hemisphere.

 

[Tanya Sharma]

Excellent thinking TSny !

Got the correct answer .

And , yes ,its quite late here . But it is always a pleasure interacting with you .

 

[TSny]

OK. I guess we'll let Chet worry about the balance of torques.

 

[Tanya Sharma]

 

[Chestermiller]

OK. I guess we'll let Chet worry about the balance of torques.

Yes. To find out where the force has to be applied, you first need to get the moment of the pressure distribtuion around z = 0. You might be able to determine this from knowing the moment of inertia of a semicircle, without actually doing the integration. If not, get the moment the same way that TSny indicated to get the force.

Chet

 

[Tanya Sharma]

Hello,

Also think about the effect of external atmospheric pressure acting on the outer curved surface of the hemisphere.

Could you please explain as to why the force exerted by external atmospheric pressure acting on the outer curved surface of the hemisphere would be P_atmπR² ?

 

[Chestermiller]

Hello,Could you please explain as to why the force exerted by external atmospheric pressure acting on the outer curved surface of the hemisphere would be P_atmπR² ?

The external atmospheric pressure acts perpendicular to the outer curved surface at each location on the surface. See what you get if you integrate this (vectorially) over the entire curved surface area of the hemisphere.

Chet

 

[TSny]

Could you please explain as to why the force exerted by external atmospheric pressure acting on the outer curved surface of the hemisphere would be P_atmπR² ?

Chet's method will nail it.

A conceptual argument can be made that might or might not satisfy you. Imagine the atmosphere as a static fluid. Consider a hemispherical volume of the atmosphere with the flat surface of the volume oriented vertically. Consider the forces acting on the flat and curved surfaces of the volume due to the surrounding atmosphere. Argue that these forces must add to zero.

 

[Tanya Sharma]

The external atmospheric pressure acts perpendicular to the outer curved surface at each location on the surface. See what you get if you integrate this (vectorially) over the entire curved surface area of the hemisphere.

Chet

Do you mind showing how you would arrive at the result using above approach .

 

[Tanya Sharma]

A conceptual argument can be made that might or might not satisfy you. Imagine the atmosphere as a static fluid. Consider a hemispherical volume of the atmosphere with the flat surface of the volume oriented vertically. Consider the forces acting on the flat and curved surfaces of the volume due to the surrounding atmosphere. Argue that these forces must add to zero.

Yes ,that makes sense if we have same fluid on the flat and curved surfaces . But in the OP we have different fluids .

Can you think of an argument considering only the curved surface just like you did in post#8 ?

 

[TSny]

Yes ,that makes sense if we have same fluid on the flat and curved surfaces . But in the OP we have different fluids .

The external atmospheric force acting on one of the hemispherical curved surfaces of the sphere filled with water is independent of what fluid is inside the sphere.

The left figure below shows a region of the atmosphere that has the same shape as a hemisphere of the sphere filled with water. The arrows indicate the external atmospheric force acting on the flat and curved surfaces of this portion of the atmosphere. The figure on the right is the sphere filled with water and the arrow indicates the external atmospheric force acting on the curved portion of one of the hemispheres of the sphere. All three forces F are equal. The force on the far left is easy to calculate.