- #1
Myslius
- 120
- 5
Suppose we have a spacetime diagram like this:
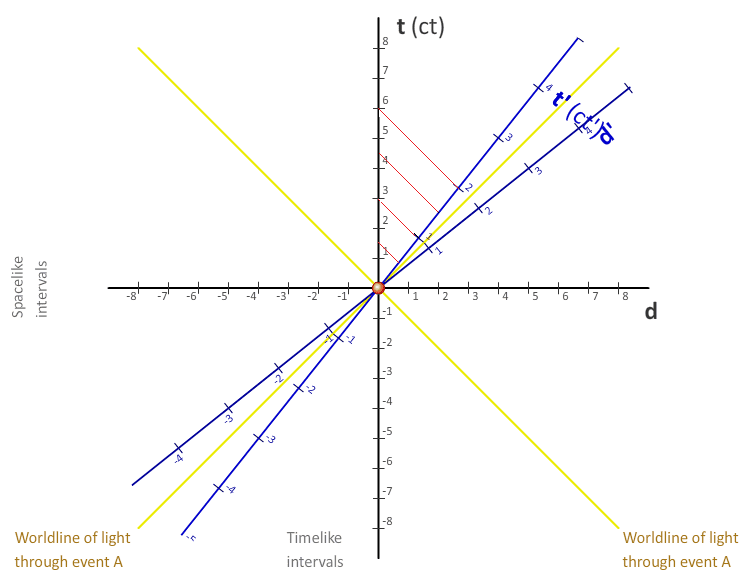
Red lines indicating light travel from the moving object to the observer.
Object is moving at the speed of 0.8c. At this speed we have:
Lorentz factor 1/√(1 - v2/c2)=1/0.6=1.66(6)
Relativistic Doppler effect √((1 + β) / (1 - β)) = 3
My question is what does the observer see?
According to this diagram At time t=3 (let's say year) observer sees object 1 year old. At t=6, 2 years old. 6/2=3 and we get Doppler effect.
As far as i know moving at 0.8c speed in no matter what direction relative to the observer results in time ticking at the speed 0.6 (or 1.66(6) slower).
Suppose at t=6 (t'=2) object starts to move towards the observer (same speed).
At t=6, object should arrive to the observer, and be 3.6 years old.
But how's that possible?
How could it be that observer sees the object at time t=6 at both places: arrived, and just starting to making a turn?
I don't understand.
Red lines indicating light travel from the moving object to the observer.
Object is moving at the speed of 0.8c. At this speed we have:
Lorentz factor 1/√(1 - v2/c2)=1/0.6=1.66(6)
Relativistic Doppler effect √((1 + β) / (1 - β)) = 3
My question is what does the observer see?
According to this diagram At time t=3 (let's say year) observer sees object 1 year old. At t=6, 2 years old. 6/2=3 and we get Doppler effect.
As far as i know moving at 0.8c speed in no matter what direction relative to the observer results in time ticking at the speed 0.6 (or 1.66(6) slower).
Suppose at t=6 (t'=2) object starts to move towards the observer (same speed).
At t=6, object should arrive to the observer, and be 3.6 years old.
But how's that possible?
How could it be that observer sees the object at time t=6 at both places: arrived, and just starting to making a turn?
I don't understand.
Last edited: