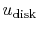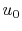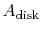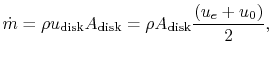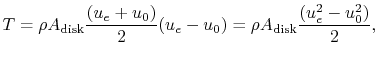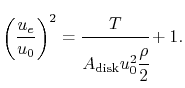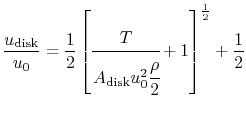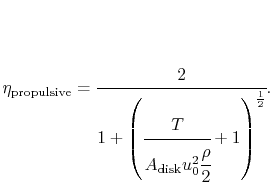Minute physics video: Why Are Airplane Engines So Big?

[Dusan Stan]

The video shows some optimisations on the turbofan engine and reaches the conclusion it needs to be about 4m.
The premise is that accelerating more air a little is more efficient than accelerating less air to a higher acceleration and speed, fact mentioned in all aerodynamics books, and that "bigger" creates more drag, fact that seems valid but I cold not find any reference of propeller diameter vs. drag.
Could anybody walk me through the math presented? I have a hard time understanding it.

 

[jedishrfu]

Well here's a reference for boat propellers and drag:

http://www.ribadventure.gr/index.ph...llers-diameter-en&catid=39&Itemid=256&lang=en

and this more technical treatment from MIT:

http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node86.html

11.7.3 talks about thrust equaling drag for level flight

We generally don't measure or control

directly. Therefore, it is more useful to write our expressions in terms of flight velocity

, thrust,

, (which must equal drag for steady level flight) and propeller disk area,

.

so

from which we can obtain an expression for the exit velocity in terms of thrust and flight velocity, which are vehicle parameters:

The other parameters of interest become

and
This is the ideal (minimum) power required to drive the propeller. In general, the actual power required would be about 15% greater than this. Lastly, the propulsive efficiency is

There are several important trends that are apparent upon consideration of these equations. We see that the propulsive efficiency is zero when the flight velocity is zero (no useful work, just a force), and tends towards one when the flight velocity increases. In practice, the propulsive efficiency typically peaks at a level of around 0.8 for a propeller before various aerodynamic effects act to decay its performance as will be shown in the following section.

 

[Dusan Stan]

Thank you jedishrfu,

I got some more info on this. The propeller blades act as airfoils, lift and drag acting as thrust and torque, respectively. One would want to drive the propeller at a optimum L/D ratio, generally alpha at about 5 deg as exemplified by Clark Y airfoil characteristics ( http://airfoiltools.com/airfoil/details?airfoil=clarky-il, see cl/cd vs alpha graph)
For a specific thrust to be generated, at optimum L/D, the blade geometry is set, the blade length and chord need to have certain dimensions, the prop having a certain diameter.
Having a bigger propeller giving similar thrust, it needs to be driven at a lower alpha, getting smaller L/D than optimum, meaning you need more torque and power, expending more energy that the optimum case.
All this is not considering that a bigger propeller is having higher wetted area and you loose energy that way too.

 

[Nidum]

There is no one single ideal diameter for the fans in turbofan engines .

The diameter is determined as part of the complex design optimisation process for a particular engine and the specific application the engine is intended for .

The fan designs used in modern turbo fans have little in common with traditional simple propeller designs .

Practical maximum diameter of the fan is usually determined by stress levels and other mechanical considerations .

With the usual design of turbofan having the fan located at the leading end of the engine the central part of the fan forms the first compressor stage for the core engine .

RR TRENT1000

 

[David Lewis]

Having a bigger propeller giving similar thrust, it needs to be driven at a lower alpha, getting smaller L/D than optimum...

The bigger prop will give more thrust for a given power input. In any case, you want the blade airfoil to operate at its max L/D angle of attack.

The performance parameter you are discussing is propeller disc loading (thrust/prop disc area). As loading goes down, efficiency goes up, assuming optimum design. The exception is airplanes going very fast. The large diameter may cause the blade tips to operate at transonic speeds, which hurts efficiency.

 

[russ_watters]

You're barking up the wrong tree here with this drag issue. The reason fans need to be as big as possible is the bigger the fan the lower the power needed to generate the thrust.

Fans generate thrust with a change in momentum: mv. But they burn power based on the imparted kinetic energy; .5mv². Since you can generate more force with a larger m or a larger v, mimimizing the kinetic energy added means using a larger m and lower v.

 

[David Lewis]

When the airplane is moving slowly, such as during takeoff, low disc loading is especially important. A higher speeds the benefit is smaller.

 

[Dusan Stan]

So far as i got the bigger the better, in theory, or at slow speeds, and I totally got this; and it makes sense, lower kinetic energy and low disk loading.
But at higher speed, a bigger propeller will have actually have a higher drag than a smaller propeller, and excluding the transonic tip speed. The cause of it being the parasitic drag being much higher than induced drag at high speed, and considering blades behaving like wings, the parasitic drag is exemplified in this graph: https://en.wikipedia.org/wiki/Parasitic_drag#/media/File:Drag_curves_for_aircraft_in_flight.svg
One would want a prop having such a diameter to have enough thrust for accelerating the plane for a reasonable takeof distance, but not as big to have an excessive drag at higher speed.

 

[russ_watters]

But at higher speed, a bigger propeller will have actually have a higher drag than a smaller propeller, and excluding the transonic tip speed. The cause of it being the parasitic drag being much higher than induced drag at high speed, and considering blades behaving like wings, the parasitic drag is exemplified in this graph: https://en.wikipedia.org/wiki/Parasitic_drag#/media/File:Drag_curves_for_aircraft_in_flight.svg

But a small propeller has to rotate faster than a big propeller, not slower. For that reason, the smaller propeller would generate more drag, not less.

 

[Dusan Stan]

@watters: A smaller propeller would need to rotate faster, but the tips speed would be the same; the bigger propeller having more surface spinning faster, so having more friction.

 

[russ_watters]

@watters: A smaller propeller would need to rotate faster, but the tips speed would be the same

That isn't true; it has to produce a higher airflow velocity, so it must either have a higher pitch (and therefore produce more drag) or higher velocity (and therefore produce more drag).

the bigger propeller having more surface spinning faster, so having more friction.

The linear/square relationship still applies: since drag is a function of velocity squared, moving less air faster produces more drag than moving more air slower.

You might try looking at some real fan performance:
http://www.tcf.com/docs/product-bulletins/tcva-axifan---vaneaxial-fans---catalog-ax100.pdf?Status=Master

The difference isn't substantial, but you will find that the efficiency of these fans goes up, not down, when you increase the fan size.

 

[Dusan Stan]

As presented here: http://www.jefflewis.net/aviation_theory-theo_prop_eff.html, two propellers, one of 8ft and another 16ft are generating similar theoretical thrust above a certain forward speed (see the last graph), calculated for same input power, but without taking into consideration the parasitic drag which would be much higher for the bigger propeller.

 

[russ_watters]

As presented here: http://www.jefflewis.net/aviation_theory-theo_prop_eff.html, two propellers, one of 8ft and another 16ft are generating similar theoretical thrust above a certain forward speed (see the last graph), calculated for same input power, but without taking into consideration the parasitic drag which would be much higher for the bigger propeller. [emphasis added]

Neither of those bolded statements are true. In a separate graph, it shows how input power goes down - radically - the larger a propeller is, for the same thrust. Applied to the graph you were referring to, it means for all of those points, the larger propeller produces that shown thrust at a much lower input power than the smaller fan.

From the link I provided above, you can look at some actual fan performance and see the same thing:

18" fan at 0.5" S.P. and 9,000 CFM: 4.75 hp, 5000 fpm. That's 29 lb of thrust.

For a 36" fan (4x the area) producing the same thrust takes twice the airflow (volumetric) at 1/2 the velocity. So that is 18,000 CFM at 3.26 hp. (Back check: 18000/13.2/32.2/3600*2512=29.6 lb thrust). Because of the increased efficiency of the bigger fan, that 3.26 hp input is actually less than what is predicted by the theory, which is 3.36 hp.

 

[Dusan Stan]

What you are saying is true for statically produced thrust, your link presents axial fans for ventilation, not really suited for aircraft.
At higher speed, the propeller diameter starts to be less important, same input power theoretically generating same amount of thrust.
Propeller efficiency:

so thrust is dependent of efficiency, power and speed, it has nothing to do with the diameter, theoretically.
So it would make sense to have same trust for the same power expended, but when you consider the loses cased by parasitic drag, you reach the conclusion that above a certain speed a smaller propeller will be practically more efficient.
The same thing is presented into this graph:

Above 150mph, almost the same thrust is generated by both propellers at same power.

 

[FactChecker]

Momentum is proportional to V (p = m*V) and energy is proportional to V² (e = 0.5*m*V²), so a low velocity gives more momentum for a given amount of energy. To propel an airplane efficiently, you want to move a greater air mass at a smaller velocity.

Of course there are a lot of other things to consider, but that is the basic advantage of larger fans.

 

[russ_watters]

Propeller efficiency:
View attachment 208055
so thrust is dependent of efficiency, power and speed, it has nothing to do with the diameter, theoretically.

Ehem: the speed of the air from the fan is inversely proportional to its diameter, for the same thrust. You are ignoring it, but it is in there.

If what you are saying were true, helicopters would have smaller blades and jets would have smaller bypass fans.

youreach the conclusion that above a certain speed a smaller propeller will be practically more efficient.

Now you are doubling-down on the wrong: even if the previous thing you said were true, that still would not be.

I'm going to be more demanding of rigor:

Above 150mph, almost the same thrust is generated by both propellers at same power.

Please quote where it says they are at the same power.

 

[Dusan Stan]

Ehem: the speed of the air from the fan is inversely proportional to its diameter, for the same thrust. You are ignoring it, but it is in there.

The speed in the efficiency calculation is not the speed of air induced by the fan, but the speed of the aircraft trough the air.

Please quote where it says they are at the same power.

It is right there in the quoted paper:"For the same horsepower, the amount of static thrust that you can produce just keeps going up with diameter. This increased thrust won't be nearly so marked throughout the whole flight, however, as the second chart below illustrates. It can be seen that even with diameters different by a factor of 2, both propellers produced nearly the same thrust at 200 mph"
And also on the graph: "400HP"

 

[Dusan Stan]

If what you are saying were true, helicopters would have smaller blades

Helicopters have indeed big rotors, and only because they need to have a lot of thrust for the static condition, when they are hovering, to increase figure of merit. Those big rotors are also an impediment for attaining high speeds, as drag increases, forward speed creating asymmetry of lift and ultimate retreating blade stall.

 

[russ_watters]

It is right there in the quoted paper:"For the same horsepower, the amount of static thrust that you can produce just keeps going up with diameter. This increased thrust won't be nearly so marked throughout the whole flight, however, as the second chart below illustrates. It can be seen that even with diameters different by a factor of 2, both propellers produced nearly the same thrust at 200 mph"
And also on the graph: "400HP"

You're right, I tripped over that, and I apologize. But as for what it means, I'll circle back to it...

The speed in the efficiency calculation is not the speed of air induced by the fan, but the speed of the aircraft trough the air.

Right again. I deal with fans every day and since they don't move, the only relevant speed is the speed of the air across the fan. Still, the difference explains the graph above: It's the reason for the convergence in the graph: as the aircraft gets faster, the aircraft's speed is a larger and larger fraction of the total speed across the fan, which reduces the benefit of the larger fan.

One thing about the equation in the video though: the drag coefficient is an assumption and a constant, not a variable with fan diameter. That means that the optimization is occurring without considering that the drag coefficient could increase with propeller diameter.

 

[FactChecker]

I see that the basic trade-off between air velocity versus air mass flow is well presented in the video and well understood. I can not fully figure out the equations in the video. I think that the main drag effect that I don't see mentioned yet is simply due to the greater weight of a larger engine requiring greater wing lift and therefore greater drag.

 

[OCR]

Those big rotors are also an impediment for attaining high speeds, as drag increases, forward speed creating asymmetry of lift and ultimate retreating blade stall.[emphasis added]

Are you confusing asymmetry of lift with dissymmetry of lift ?

Dissymmetry of lift ultimately leads to retreating blade stall... which is usually the primary limiting factor of a helicopter's airspeed...

 

[Dusan Stan]

Ha! It definitely seems that I'm confusing asymmetry and dissymmetry. I agree that the dissymmetry is the primary cause limiting the helicopter speed, but if the rotor was smaller, the retreating blade would be faster, and the stall delayed at a higher speed. All this at the expense of a lower figure of merit while hovering.

 

[DarioC]

Here is an example of how propellers work in the real world. I have a 1946 Taylorcraft. Something like a hot rod Cub if you know what that is. It has a 71 inch propeller and will climb at about 750 to 850 feet per minute depending on conditions. With a 74 inch prop it would be able to climb at up to 1500 feet per minute. Why don't I or other Taylorcraft owners use this prop?

It is because there is a trade off. The longer prop will have to be pitched at a lower pitch (angle of attack) to let the engine turn up to to the RPM where it develops maximum power in the climb. When you go to level flight the lower pitched prop does not transfer enough energy to the air at the engine rated cruise RPM and the airplane will cruise at a slower speed. More complex/expensive aircraft have variable pitch props for this reason.

It appears that by your picture at the start that you are thinking of hi-bypass turbofan engines. A shrouded fan is a whole 'nother deal. The big fans on modern jets tell us that they were designed to move as much air as possible under a wide variety of air speeds, that is takeoff, climb, and cruise. The surrounding shroud makes the fan behave quite differently from a propeller.

 

[OCR]

Something like a hot rod Cub if you know what that is.

Why, yes... yes I do. [COLOR=#black].[/COLOR]

Interesting... and you are correct about the propellers.

I have a 1946 Taylorcraft.

My brother and I had a 1946 J-3, that my dad had bought new... in 1946...

He had replaced the original Continental A65 with a Continental C90 and the wooden prop with a metal "climb" prop... actually the engine would hit the red line, and maybe a tad over, at takeoff power, but it got off the ground fast.

Here's a "not really good" picture of it taken on 2-27-2009... we sold it locally here, to a friend, on 9-10-2009...