Missing factor of 2 in an equilibrium problem

Thread starter Eggue
Start date Apr 13, 2020
Tags

Equilibrium

Click For Summary

SUMMARY

The discussion centers on a discrepancy in solving an equilibrium problem, specifically regarding a missing factor of 2 in the final answer. The correct solution, as stated in the book, is \(\frac{L}{2} + \frac{h^2}{L}\). Participants express confusion over their calculations and the use of a derivative calculator, indicating a need for clarity in the differentiation process. The conversation highlights the importance of verifying each step in mathematical problem-solving to ensure accuracy.

PREREQUISITES

Understanding of equilibrium problems in physics
Proficiency in differentiation techniques
Familiarity with derivative calculators
Basic knowledge of algebraic manipulation

NEXT STEPS

Review the principles of equilibrium in physics
Study differentiation rules and applications in calculus
Practice using derivative calculators effectively
Explore common pitfalls in algebraic problem-solving

USEFUL FOR

Students studying physics or mathematics, educators teaching calculus, and anyone seeking to improve their problem-solving skills in equilibrium scenarios.

Apr 13, 2020

Eggue

Homework Statement: A heavy horizontal girder of length L has several objects suspended from it. It is supported by a frictionless pivot at its left end and a cable of negligible weight that is attached to an I-beam at a point a distance h directly above the girder’s center. Where should the other end of the cable be attached to the girder so that the cable’s tension is a minimum?

Relevant Equations: Conditions for equilibrium

I honestly have no idea where I'm going wrong
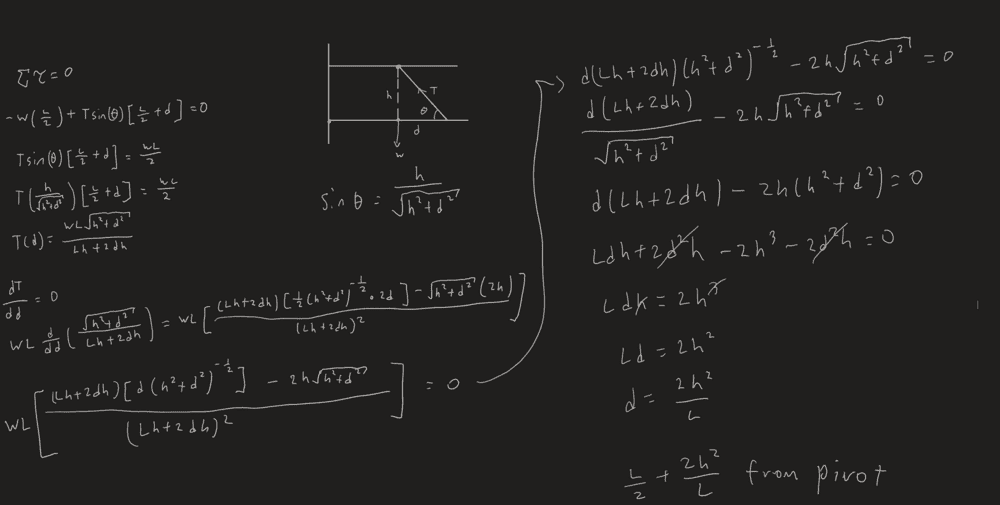
i've checked my differentiation using a derivative calculator but the answer is the same.
The answer from the book is \frac{L}{2} + \frac{h^2}{L}

Working: