MexChemE
- 237
- 54
Good evening, PF! I am supposed to model the following system. I will be using the same notation as in BSL.
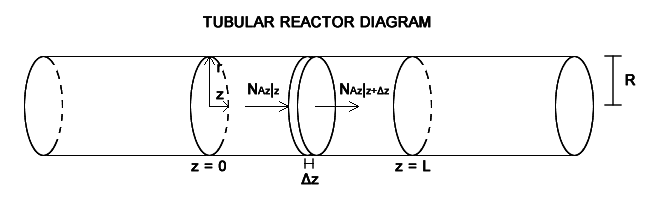
Fluid A enters the reaction zone at z = 0 at a concentration CA0. A reacts to form B in the first order reaction A → B at a rate of R_A = k_1''' C_A. We assume the whole mixture to be incompressible, with constant global C and ρ, so the mass average velocity equals the molar average velocity. Diffusion effects can not be neglected. I have to consider two situations, plug flow and laminar flow. However, the velocity profile in laminar flow only depends on the radial direction, so I only performed one mass balance for species A. The shell mass balance for species A in the volume element πR2Δz is
\pi R^2 N_{Az} |_z - \pi R^2 N_{Az} |_{z+\Delta z} - \pi R^2 \Delta z R_A = 0
Then, dividing by the whole volume and taking the limit as Δz approaches zero
\frac{d N_{Az}}{dz} + R_A = 0
The molar flux in the z direction is given by
N_{Az} = -D_{AB} \frac{dC_A}{dz} + C_A v_z
Substituting this expression in the first differential equation, we arrive at the equation which must be solved to find the concentration profile
D_{AB} \frac{d^2 C_A}{dz^2} - v_z \frac{dC_A}{dz} - k_1''' C_A = 0
I solved this equation by proposing C_A = c_1 e^{m_1 z} + c_2 e^{m_2 z} as a solution and using the auxiliary equation of the form
D_{AB} m^2 - v_z m - k_1''' = 0
Solving the above equation, I got
m_1 = \frac{v_z + \sqrt{v_z^2 + 4D_{AB} k_1'''}}{D_{AB}^2}
m_2 = \frac{v_z - \sqrt{v_z^2 + 4D_{AB} k_1'''}}{D_{AB}^2}
Using the following boundary conditions in order to find the constants of integration
B.C. 1: z = 0; CA = CA0
B.C. 2: z = L; CA = CA1
I arrived at the concentration profile of A
C_A = \left( \frac{C_{A0} e^{m_2 L} - C_{A1}}{e^{m_2 L} - e^{m_1 L}} \right) e^{m_1 z} + \left( \frac{C_{A1} - C_{A0} e^{m_1 L}}{e^{m_2 L} - e^{m_1 L}} \right) e^{m_2 z}
Now, in the plug flow case, vz is a constant and we have nothing to worry about when using the model. In the laminar flow case, vz is a function of r, so, does that mean that CA becomes a function of r and z? We could also use the average velocity <vz>, which is also a constant.
Also, I have questions about the relationship between NA and NB. Stoichiometry tells us that N_A = - N_B, however, given the geometric nature of molar fluxes, that would mean that B flows in the negative z direction, and this is not the case. That would also mean x_A(N_A + N_B) = 0, thus no convective term in the modified form of Fick's first law N_{Az} = -D_{AB} \frac{dC_A}{dz} + x_A(N_A + N_B). Right now, my guess is that N_A = N_B, but I'm not sure. I'm still struggling to comprehend the physical interpretation of the mathematics of mass transfer.
This is it, for the moment. Thanks in advance for any kind of input!
Fluid A enters the reaction zone at z = 0 at a concentration CA0. A reacts to form B in the first order reaction A → B at a rate of R_A = k_1''' C_A. We assume the whole mixture to be incompressible, with constant global C and ρ, so the mass average velocity equals the molar average velocity. Diffusion effects can not be neglected. I have to consider two situations, plug flow and laminar flow. However, the velocity profile in laminar flow only depends on the radial direction, so I only performed one mass balance for species A. The shell mass balance for species A in the volume element πR2Δz is
\pi R^2 N_{Az} |_z - \pi R^2 N_{Az} |_{z+\Delta z} - \pi R^2 \Delta z R_A = 0
Then, dividing by the whole volume and taking the limit as Δz approaches zero
\frac{d N_{Az}}{dz} + R_A = 0
The molar flux in the z direction is given by
N_{Az} = -D_{AB} \frac{dC_A}{dz} + C_A v_z
Substituting this expression in the first differential equation, we arrive at the equation which must be solved to find the concentration profile
D_{AB} \frac{d^2 C_A}{dz^2} - v_z \frac{dC_A}{dz} - k_1''' C_A = 0
I solved this equation by proposing C_A = c_1 e^{m_1 z} + c_2 e^{m_2 z} as a solution and using the auxiliary equation of the form
D_{AB} m^2 - v_z m - k_1''' = 0
Solving the above equation, I got
m_1 = \frac{v_z + \sqrt{v_z^2 + 4D_{AB} k_1'''}}{D_{AB}^2}
m_2 = \frac{v_z - \sqrt{v_z^2 + 4D_{AB} k_1'''}}{D_{AB}^2}
Using the following boundary conditions in order to find the constants of integration
B.C. 1: z = 0; CA = CA0
B.C. 2: z = L; CA = CA1
I arrived at the concentration profile of A
C_A = \left( \frac{C_{A0} e^{m_2 L} - C_{A1}}{e^{m_2 L} - e^{m_1 L}} \right) e^{m_1 z} + \left( \frac{C_{A1} - C_{A0} e^{m_1 L}}{e^{m_2 L} - e^{m_1 L}} \right) e^{m_2 z}
Now, in the plug flow case, vz is a constant and we have nothing to worry about when using the model. In the laminar flow case, vz is a function of r, so, does that mean that CA becomes a function of r and z? We could also use the average velocity <vz>, which is also a constant.
Also, I have questions about the relationship between NA and NB. Stoichiometry tells us that N_A = - N_B, however, given the geometric nature of molar fluxes, that would mean that B flows in the negative z direction, and this is not the case. That would also mean x_A(N_A + N_B) = 0, thus no convective term in the modified form of Fick's first law N_{Az} = -D_{AB} \frac{dC_A}{dz} + x_A(N_A + N_B). Right now, my guess is that N_A = N_B, but I'm not sure. I'm still struggling to comprehend the physical interpretation of the mathematics of mass transfer.
This is it, for the moment. Thanks in advance for any kind of input!
Last edited: