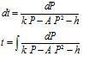NZBRU
- 19
- 0
Does anyone know how to solve dP/dt = k P - A P2 - h for P. I understand partial fractions are needed and I have already solved dP/dt = k P - A P2. Is anyone able to solve it, Cheers NZBRU.