Molar heat capacity and Degrees of freedom

[Effect]

Homework Statement

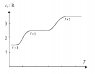
The diagram shows the molar heat capacity of an ideal diatomic gas and the number of degrees of freedom at different temperatures. Explain why there are 3 discrete plateaus and why the curve is smooth and leaning between them.

Homework Equations

-

The Attempt at a Solution

For f=3 degrees of freedom we have translational motion, for f=5 we have also rotational motion and for f=7 there is also vibrational motion.

The equipartition theorem states that if a system is in equilibrium, there is an average energy of (1/2)kT per molecule or (1/2)RT per mole associated with each degree of freedom. The equipartition theorem fails if the thermal energy that can be transferred in collisions is smaller than the energy gap between quantized energy levels.

For example, the energy that can be transferred between colliding gas molecules is of the order of kT, the
typical thermal energy of a molecule. Hence in that case there are three distinct plateaus that represents the change in accordance with the quantized energy levels.

That explains why there are 3 discrete plateaus. What I wonder is why is the curve smooth and leaning between these plateaus? Could someone please explain that?

 

[Effect]

A fast response to this would be appreciated

 

[haruspex]

The equipartition theorem fails if the thermal energy that can be transferred in collisions is smaller than the energy gap between quantized energy levels.

For example, the energy that can be transferred between colliding gas molecules is of the order of kT, the
typical thermal energy of a molecule. Hence in that case there are three distinct plateaus that represents the change in accordance with the quantized energy levels.

Doesn't seem to me you've really explained why the number of degrees of freedom increases at certain temperature thresholds. E.g., why does rotation have a higher threshold than translation? (Btw, I don't know the answer to that.)

why is the curve smooth and leaning between these plateaus? Could someone please explain that?

Do all molecules have the same energy at once?