- #1
Jason234578
- 1
- 0
- Homework Statement
- Determine the moment of the force around point O
- Relevant Equations
- M=fd
G'day.
I have a problem with my statics work, i understand its probably quite simple but I am having trouble in my understanding.
Essentially problems make more sense to me by using the component method, although in saying that i understand this problem would be quite a lot more simple were i to approach it without the component method.
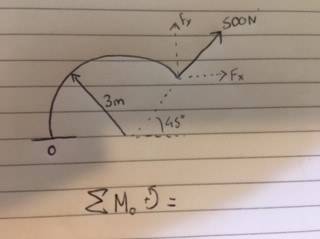 heres the vector diagram for the problem,
heres the vector diagram for the problem,
 this is the answer for the sum of the components, but I am confused why Fx is negative and why Fy is being multiplied by 3+3cos45, i understand the barebones equation for the moment is M=fd(perpendicular), but from my understanding Fx would be acting in the positive (right) direction.
this is the answer for the sum of the components, but I am confused why Fx is negative and why Fy is being multiplied by 3+3cos45, i understand the barebones equation for the moment is M=fd(perpendicular), but from my understanding Fx would be acting in the positive (right) direction.
I have a problem with my statics work, i understand its probably quite simple but I am having trouble in my understanding.
Essentially problems make more sense to me by using the component method, although in saying that i understand this problem would be quite a lot more simple were i to approach it without the component method.