Niall
- 4
- 0
Im needing to calculate the Zxx and Yxx for 2 shapes.
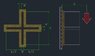
The shapes are an H profile and a + profile however its not the basic profiles I am needing but the moment of inertia for the weld profile surrounding them as the theory is they are welded to a vertical metal surface then a load is applied.
It is the hatched area of the two attachments which shows it more clearly.
I have formula for working out the basic shapes and I had hoped to be able to simply subtract the smaller profile from the larger profile but that doesent appear to work.
I can get the answers from Autocad and Inventor but I need to be able to justify how I got my answers and I am just not getting anywhere with it.
Any help would be appreciated.
The shapes are an H profile and a + profile however its not the basic profiles I am needing but the moment of inertia for the weld profile surrounding them as the theory is they are welded to a vertical metal surface then a load is applied.
It is the hatched area of the two attachments which shows it more clearly.
I have formula for working out the basic shapes and I had hoped to be able to simply subtract the smaller profile from the larger profile but that doesent appear to work.
I can get the answers from Autocad and Inventor but I need to be able to justify how I got my answers and I am just not getting anywhere with it.
Any help would be appreciated.