I am sorry you are still confused. I'm probably making it worse for you.
The issue may be this:
There are 2 different sign conventions,
-- one for external moments, and
-- one for internal moments.
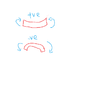
Let's look at the internal moments first. Internal moments exist within the beam itself and are caused by the applied loadings.. The sign of those moments have been I hope well established already in the prior posts, that is to say, internal moments that cause the beam to deflect concave upward (like a smiley face) are positive, while internal moments that cause the beam to deflect concave downward (upside down U) are negative. The cw or ccw direction of these moments are as established in your famous third attachment on post 1. These signs by the way...plus or minus...will come directly from your moment diagram without having to look at the curved shape of the deflected beam...provided you draw the moment diagram correctly, however.
So speaking of the moment diagram , now let's look at the external moments. External moments are either directly applied moments (couples) or fixed end support reaction moments (FEM). Both types of these external moments have the convention of positive if they are clockwise, or negative if they are counterclockwise. This is unlike the internal moments where clockwise moments can be plus or minus depending on which side of the beam section you are looking at. But again, clockwise external moments are always positive.
So in conclusion, looking your original problem, the internal moment in the beam at the right end is clockwise on a left hand section and thus a negative 12.86, and since the FEM is an external clockwise moment, it is a plus 12.86, which closes your moment diagram to 0.
Well , whaddya think?



![IMG_20170421_002516[1].jpg](/data/attachments/179/179110-eefdd129b349c4dddb9aad72e6406a80.jpg?hash=7v3RKbNJxN)