Momentum Thrust of an Over-Expanded Rocket Nozzle

[BrandonBerchtold]

TL;DR Summary

Momentum Thrust of Over-Expanded Rocket Nozzle

Hi All,
I'm trying to get a better understanding of the momentum thrust given by an over-expanded rocket nozzle (I realize this case voids the isentropic flow assumption used for the 1D isentropic gas expansion equations typically used for rocket engine design since the normal shock is not an isentropic process, but figuring out how momentum works in a supersonic flow is really messing with my brain right now).

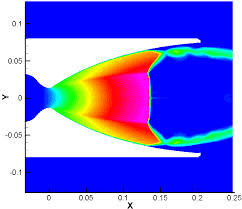
Momentum thrust is given by the mass flow rate of propellants times the exit plane velocity, so when the flow mach number plot looks like the image below, what velocity is used as the "exit velocity"? Is the nozzle assumed to stop right before the normal shock, therefore using the maximum attained flow velocity before the shock as the "exit velocity", or is the exit velocity taken as the velocity across the exit plane downstream of the normal shock?

My reasoning is that since the flow is supersonic, no information may travel upstream, so if the flow slows down within the nozzle due to a shock, it can't really affect the nozzle walls upstream of the shock, therefore the exit velocity would be the max velocity before the normal shock. Is my reasoning incorrect?

View attachment 272099 [Source: https://www.mas.bg.ac.rs/_media/istrazivanje/fme/vol40/3/03_vzmijanovic.pdf]

 

[mfb]

There are two ways to study this:

- by forces on the nozzle. Probably the more complicated way.
- by conservation of total momentum. Only the final exit velocity (after the nozzle) matters - and the speed of surrounding air if it gets accelerated backwards.

 

[NatSusan]

Hi there,

Your reasoning is correct. The exit velocity in this case would be the maximum velocity before the normal shock. This is because, as you mentioned, once the flow is supersonic, no information can travel upstream, so the shock cannot affect the nozzle walls upstream of it. Therefore, the exit velocity would be the maximum velocity attained before the shock.

I hope this helps clarify your understanding of momentum thrust in over-expanded rocket nozzles. Let me know if you have any further questions.