Motion in 2D: Find Which Ball Hits Circle First?

[lmao2plates]

Homework Statement

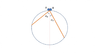
Two balls A and B simultaneously start to roll down without friction along
two different chords of a circle as shown in the figure. Find which ball will
hit the circle first? (image attached)

2. The attempt at a solution
I have divided the velocity of the balls into vector components, for A being mgcos(αA) and B being mgcos(αB).
Since αA > αB, and being in the first quadrant of the unit circle, I have concluded that mgcos(αA) < mgcos(αB).

However, I am stuck at how to determine which one will hit the circle first since B has to travel a longer distance that A.

I appreciate your assistance.

 

[BvU]

First of all: mgcos(α_A) is not a velocity but a force (check the dimensions) !

Then: as a helper, I am used to finding the relevant equations that are needed to solve the problem listed under 2). Relevant equations. What do you have available to deal with this problem?

Under 3). attempt at solution, we then look for clues as to what is preventing the poster to proceed. You state why you are stuck, but is it because you can't calculate how long the trajectories are ?

A few hints:
mgcos(α_A) looks like it is independent of time, so you have a constant force. What releveant equation can you use to show that the equations for constant acceleration apply here ? What are these equations ?
Is there anything else (apart from the trajectory lengths) that you need ?

 

[lmao2plates]

Ahhh. Thanks for correcting me, it is indeed a force.

So the only constant acceleration equation that is independent from time is v² = v²₀ + 2ax

I will continue from here and update on my progress.

Thank you.

 

[BvU]

So the only constant acceleration equation that is independent from time

Looks as if you are going the wrong way. I mean: the acceleration is constant. The motion does involve time (after all they want to know which one arrives first).
With constant acceleration, linear motion can be described with which equations ?

 

[lmao2plates]

Relevant equations:

1) V=V₀ + at

2) X=X₀ + V₀*t + 1/2a(t²)

3) X=X₀ + 1/2(V + V₀)t

4) V²=V₀²+2a(X - X₀)

How should I work with this?

 

[BvU]

Haha. recipe for success:
1 .Discard the ones you don't expect you to give a good answer.
2. Then pick the one for which you have what's needed and thaty you eexpect to give you the desired result.
3. Go to work
4. If succesful, done; if not go back to step 2. If all exhausted, go back to step 1.
5. If all exhausted and still not succesful, expand collection of relevant equations.
All this of course after having
1.) clearly stated the problem and listed all the variables and given/known data (with the correct units)

More seriously:
what do you think of your number 1) ? I think ít has nothing on X
what do you think of your number 2) ? Anything in there you don't know ? What are all the variables, precisely?
what do you think of your number 3) ? I think ít has nothing on a (and it is about some average speed, which is not very useful here) Where does it come from ? This is one that I suspect isn't applicable here...
what do you think of your number 4) ? Where does it come from ? I think ít has nothing on t, so it won't tell us which one got there first !

 

[lmao2plates]

So using 2)

for both balls it becomes:

X = 0 + 0(t) + 1/2(a)(t^2)
X = 1/2(a)(t^2)
t^2 = X/(1/2a)

Since X_A < X_B and a_A < a_B ...

It seems like I have hit another sticking point.

 

[BvU]

Write out what x_A and x_B are

As I asked "write out all the variables, precisely". You already have a_A and a_B