etotheipi
@TSny pointed out your error, but I'd like to provide a little more context just because in my experience pulleys are notoriously poorly explained in school.
Although this problem tells us to neglect friction between the string and the pulley, it's more instructive to consider the general case where there is friction (which we will assume to be limiting), and then - if you want - to set ##\mu = 0## afterwards.
Suppose that the section of string in contact with the pulley subtends an angle ##(\pi - 2\alpha) / 2##, and superimpose a co-ordinate system whose ##y##-axis coincides with the axis of symmetry.
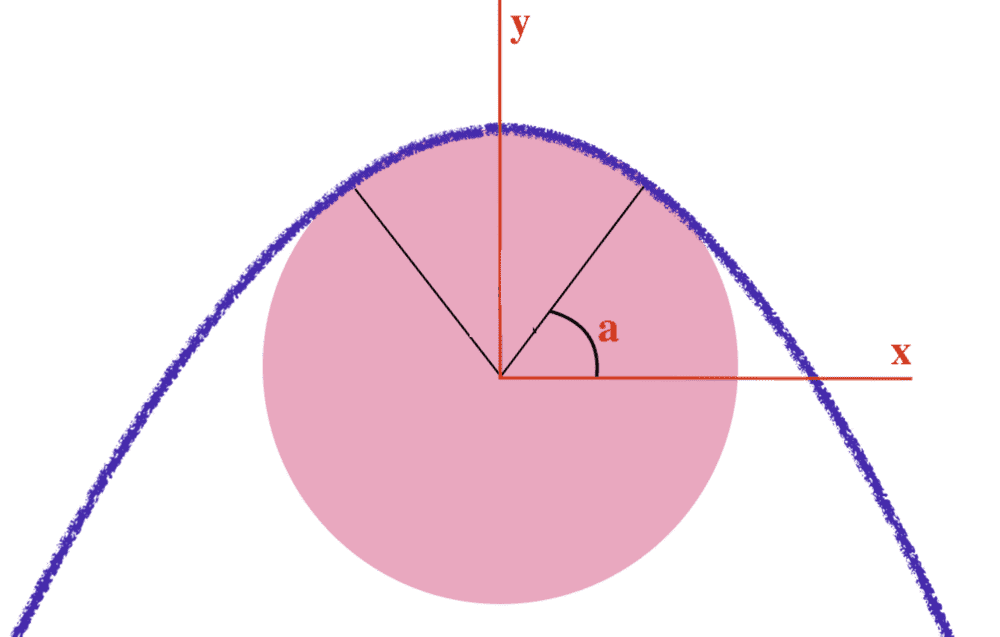
Now consider a small element at an angle ##\theta## to the ##x##-axis.
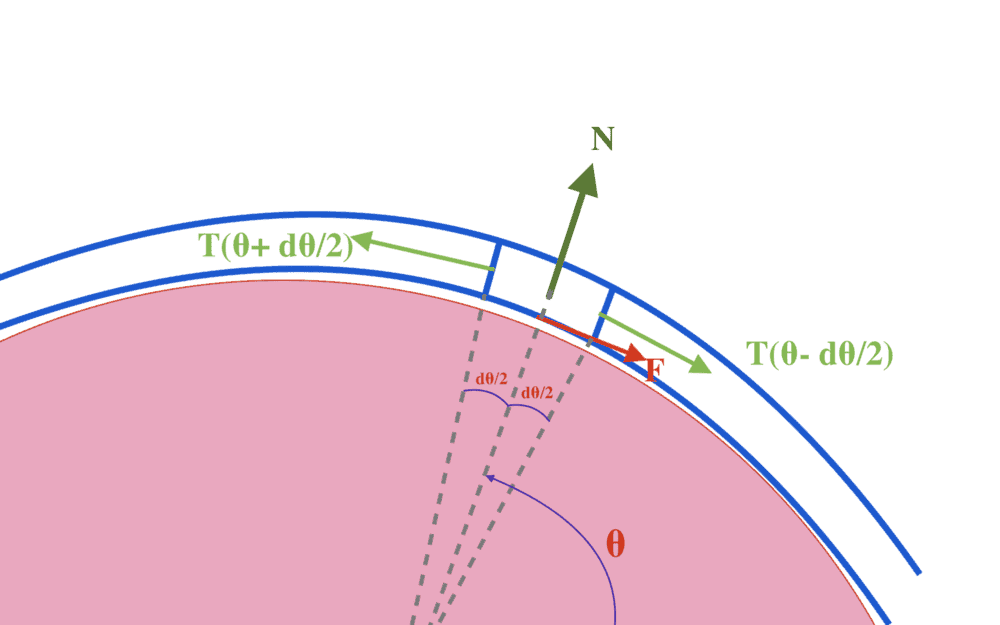
Balance the forces acting on the element tangential to the surface:$$T \left(\theta + \frac{d\theta}{2} \right) \cos{ \frac{d\theta}{2}} - T \left(\theta - \frac{d\theta}{2} \right) \cos{\frac{d\theta}{2}} - \mu N(\theta) = 0$$Balance the forces on the element normal to the surface:$$N(\theta) - T \left(\theta + \frac{d\theta}{2} \right) \sin{\frac{d\theta}{2}} - T \left(\theta - \frac{d\theta}{2} \right) \sin{\frac{d\theta}{2}} = 0$$You can simplify this by writing ##\cos{\frac{d\theta}{2}} \sim 1 - \frac{d\theta^2}{2}## and ##\sin{\frac{d\theta}{2}} \sim \frac{d\theta}{2}##, and further by noticing that
$$T \left(\theta + \epsilon \right) = T(\theta) + T'(\theta) \epsilon + \mathcal{O}(\epsilon^2)$$If you write out those expansions then you'll obtain that, to first order in ##d\theta##,$$T'(\theta) d\theta = \mu N(\theta) \ \ \ (1)$$and$$N(\theta) = T(\theta) d\theta \ \ \ (2)$$don't be put off by the fact that what I called ##N(\theta)## is actually differential form! You can just combine to get the differential equation$$T'(\theta) = \mu T(\theta)$$and you may be aware that this has a solution ##T(\theta) = T(0)e^{\mu \theta}##; i.e. in the limiting case, the tension increases exponentially around the pulley. [Although the string is not in contact with the pulley at ##\theta = 0##, you can just view ##T(0)## as some constant fixing the solution].
We're not there yet, though, because we want to ultimately work out the force that the pulley exerts on the string - and then by NIII, the force that the string exerts on the pulley. For example, the ##y##-component of the contact force the pulley exerts on the string may be computed via an integral$$
\begin{align*}
\int_{\alpha}^{\pi - \alpha} dF_y = \int_{\alpha}^{\pi - \alpha}\left[ N(\theta) \sin{\theta} - \mu N(\theta) \cos{\theta} \right] &= \int_{\alpha}^{\pi - \alpha} (\sin{\theta} - \mu \cos{\theta}) T(\theta) d\theta \\ \\
&= T(0) \cos{\alpha} \left[ e^{\mu(\pi - \alpha)} + e^{\mu \alpha} \right]
\end{align*}$$But ##T(0)e^{\mu(\pi - \alpha)} = T(\pi - \alpha)## and ##T(0)e^{\mu \alpha} = T(\alpha)##, so you can see the y-component of force that the pulley exerts on the string is$$F_y = T(\alpha) \cos{\alpha} + T(\pi - \alpha) \cos{\alpha}$$and thus by NIII, the string exerts $$\tilde{F}_y = -T(\alpha) \cos{\alpha} - T(\pi - \alpha) \cos{\alpha}$$on the pulley, or in other words, exactly equivalent to if the pulley were acted upon by two forces ##T(\alpha)## and ##T(\pi - \alpha)## in the direction of the string, even though the tension forces don't actually act on the pulley (they only act on neighbouring bits of string!). You can [and should!] do a similar calculation for the ##x##-direction.
Another, perhaps more intuitive, way to think about it is to consider the string in contact with the pulley as part of the "pulley+string-in-contact-with-pulley system". Then, the force this system due to the string is just that exerted by the external axial tension on the bit of the string in contact with the pulley.
Although this problem tells us to neglect friction between the string and the pulley, it's more instructive to consider the general case where there is friction (which we will assume to be limiting), and then - if you want - to set ##\mu = 0## afterwards.
Suppose that the section of string in contact with the pulley subtends an angle ##(\pi - 2\alpha) / 2##, and superimpose a co-ordinate system whose ##y##-axis coincides with the axis of symmetry.
Now consider a small element at an angle ##\theta## to the ##x##-axis.
Balance the forces acting on the element tangential to the surface:$$T \left(\theta + \frac{d\theta}{2} \right) \cos{ \frac{d\theta}{2}} - T \left(\theta - \frac{d\theta}{2} \right) \cos{\frac{d\theta}{2}} - \mu N(\theta) = 0$$Balance the forces on the element normal to the surface:$$N(\theta) - T \left(\theta + \frac{d\theta}{2} \right) \sin{\frac{d\theta}{2}} - T \left(\theta - \frac{d\theta}{2} \right) \sin{\frac{d\theta}{2}} = 0$$You can simplify this by writing ##\cos{\frac{d\theta}{2}} \sim 1 - \frac{d\theta^2}{2}## and ##\sin{\frac{d\theta}{2}} \sim \frac{d\theta}{2}##, and further by noticing that
$$T \left(\theta + \epsilon \right) = T(\theta) + T'(\theta) \epsilon + \mathcal{O}(\epsilon^2)$$If you write out those expansions then you'll obtain that, to first order in ##d\theta##,$$T'(\theta) d\theta = \mu N(\theta) \ \ \ (1)$$and$$N(\theta) = T(\theta) d\theta \ \ \ (2)$$don't be put off by the fact that what I called ##N(\theta)## is actually differential form! You can just combine to get the differential equation$$T'(\theta) = \mu T(\theta)$$and you may be aware that this has a solution ##T(\theta) = T(0)e^{\mu \theta}##; i.e. in the limiting case, the tension increases exponentially around the pulley. [Although the string is not in contact with the pulley at ##\theta = 0##, you can just view ##T(0)## as some constant fixing the solution].
We're not there yet, though, because we want to ultimately work out the force that the pulley exerts on the string - and then by NIII, the force that the string exerts on the pulley. For example, the ##y##-component of the contact force the pulley exerts on the string may be computed via an integral$$
\begin{align*}
\int_{\alpha}^{\pi - \alpha} dF_y = \int_{\alpha}^{\pi - \alpha}\left[ N(\theta) \sin{\theta} - \mu N(\theta) \cos{\theta} \right] &= \int_{\alpha}^{\pi - \alpha} (\sin{\theta} - \mu \cos{\theta}) T(\theta) d\theta \\ \\
&= T(0) \cos{\alpha} \left[ e^{\mu(\pi - \alpha)} + e^{\mu \alpha} \right]
\end{align*}$$But ##T(0)e^{\mu(\pi - \alpha)} = T(\pi - \alpha)## and ##T(0)e^{\mu \alpha} = T(\alpha)##, so you can see the y-component of force that the pulley exerts on the string is$$F_y = T(\alpha) \cos{\alpha} + T(\pi - \alpha) \cos{\alpha}$$and thus by NIII, the string exerts $$\tilde{F}_y = -T(\alpha) \cos{\alpha} - T(\pi - \alpha) \cos{\alpha}$$on the pulley, or in other words, exactly equivalent to if the pulley were acted upon by two forces ##T(\alpha)## and ##T(\pi - \alpha)## in the direction of the string, even though the tension forces don't actually act on the pulley (they only act on neighbouring bits of string!). You can [and should!] do a similar calculation for the ##x##-direction.
Another, perhaps more intuitive, way to think about it is to consider the string in contact with the pulley as part of the "pulley+string-in-contact-with-pulley system". Then, the force this system due to the string is just that exerted by the external axial tension on the bit of the string in contact with the pulley.
Last edited by a moderator: