- #1
songoku
- 2,294
- 325
- Homework Statement
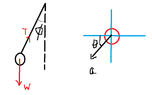
- A person, holding a simple pendulum, stands on a moving platform inclined at 30 degrees to horizontal. When the platform is at rest, the period of the pendulum is 2 s. When the platform moves with constant acceleration ##2 m/s^2##, the period will be
a) 2.36 s
b) 2 s
c) 1.64 s
d) 2.11 s
e) 1.89 s
- Relevant Equations
- ##T=2\pi \sqrt{\frac{L}{\text{apparent gravity}}}##
When the platform moves with constant acceleration, the equation of Newton's 2nd law of motion is
Forward force - W sin 30o = m.a
Forward force = m (a + g sin 30o) ⇒ apparent gravity = a + g sin 30oFinal period of pendulum = ##\sqrt{\frac{g}{a+g \sin 30^{0}}} \times 2 = 2.38 s##
Is this correct? Thanks
Forward force - W sin 30o = m.a
Forward force = m (a + g sin 30o) ⇒ apparent gravity = a + g sin 30oFinal period of pendulum = ##\sqrt{\frac{g}{a+g \sin 30^{0}}} \times 2 = 2.38 s##
Is this correct? Thanks