cjk2
- 2
- 0
For those who don't know there exists a sport called robot combat. Two robots enter an area and fight until one is unable to move anymore or its owner taps out. I have a novel idea for a weapon for a robot but I am unsure if the maths works out so that it will be practical.
Suppose I take a metal blade that is 6" long and spin it about its center of mass at 12000rpm. This will cause the tips to experience about 10000G of force(maybe not the right word). The blade does not spin around a simple hub but rather has a rounded slot cut slightly off center (see the attached picture). The idea is that when the blade bumps the other robot the blade is allowed to slide so that its center of mass is no longer in the same place as the center of the hub that it rotates on. Centrifugal(maybe not the right word) force will cause the blade to be pulled all the way to the end of its travel and the blade will hit the other side of the hub. This will cause the blade to be unbalanced but it will also cause the effective radius of the blade to become larger. In the robot combat world this would be a big advantage because you can never seem to have enough "bite".
Here is the problem: I built a prototype of this device and it seems that sometimes the blade does not slide much in the half a revolution it has before it hits the enemy robot. At 12000rpm the blade only has 0.0025 seconds between initial tap and huge whack. Suppose the blade is initially knocked in 0.01 inchs with respect to the hub. If the blade weighs 60 grams how far will it advance in the 0.0025 seconds before the business end makes it half a turn around that hits the other robot? I suspect for my purposes some simplifications to the problem can be made as I do not need absolute accuracy. For example we can probably assume the speed of the blade does not vary and the tips of the blade always see 10000G.
The blade is 6 inches long, 0.094 inches thick and 1 inch wide. It weighs about 60 grams and is made of carbon steel. It does have some holes it it make it lighter but they are not near the ends.
I hope I have explained this well enough to be understood. Please see the attached drawing for additional clarification. My attempt to solve this problem so far has been met with failure. I tried to approximate a solution using the formula D=0.5*a*t^2 but this does not account for the fact that as the bar slides the imbalance becomes greater and greater. I suspect the solution will have a t^3 term in it. I think this problem is similar to a situation where a weight is dropped but the gravity becomes stronger the further it falls.
http://i.imgur.com/iDdQ4z5.png
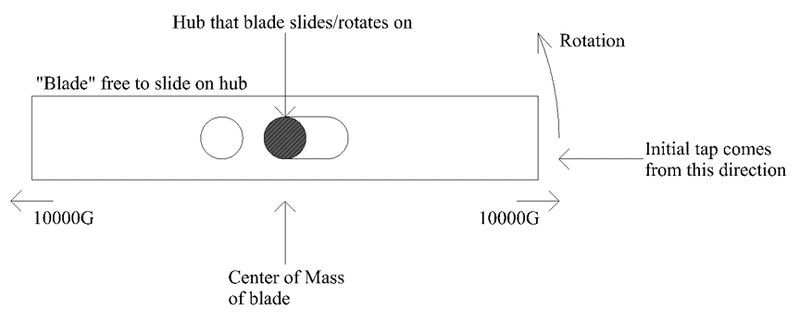
Suppose I take a metal blade that is 6" long and spin it about its center of mass at 12000rpm. This will cause the tips to experience about 10000G of force(maybe not the right word). The blade does not spin around a simple hub but rather has a rounded slot cut slightly off center (see the attached picture). The idea is that when the blade bumps the other robot the blade is allowed to slide so that its center of mass is no longer in the same place as the center of the hub that it rotates on. Centrifugal(maybe not the right word) force will cause the blade to be pulled all the way to the end of its travel and the blade will hit the other side of the hub. This will cause the blade to be unbalanced but it will also cause the effective radius of the blade to become larger. In the robot combat world this would be a big advantage because you can never seem to have enough "bite".
Here is the problem: I built a prototype of this device and it seems that sometimes the blade does not slide much in the half a revolution it has before it hits the enemy robot. At 12000rpm the blade only has 0.0025 seconds between initial tap and huge whack. Suppose the blade is initially knocked in 0.01 inchs with respect to the hub. If the blade weighs 60 grams how far will it advance in the 0.0025 seconds before the business end makes it half a turn around that hits the other robot? I suspect for my purposes some simplifications to the problem can be made as I do not need absolute accuracy. For example we can probably assume the speed of the blade does not vary and the tips of the blade always see 10000G.
The blade is 6 inches long, 0.094 inches thick and 1 inch wide. It weighs about 60 grams and is made of carbon steel. It does have some holes it it make it lighter but they are not near the ends.
I hope I have explained this well enough to be understood. Please see the attached drawing for additional clarification. My attempt to solve this problem so far has been met with failure. I tried to approximate a solution using the formula D=0.5*a*t^2 but this does not account for the fact that as the bar slides the imbalance becomes greater and greater. I suspect the solution will have a t^3 term in it. I think this problem is similar to a situation where a weight is dropped but the gravity becomes stronger the further it falls.
http://i.imgur.com/iDdQ4z5.png