What is the Effect of Isothermal Movement on Internal Energy of a Gas?

[L_landau]

Homework Statement

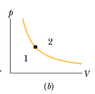
The dot in Fig. 19-18b represents the initial state of a gas, and the isotherm through the dot divides the p-V diagram into regions 1 and 2. For the following processes, determine whether the change Eint in the internal energy of the gas is positive, negative, or zero: (a) the gas moves up along the isotherm, (b) it moves down along the isotherm, (c) it moves to anywhere in region 1, and (d) it moves to anywhere in region 2.

Homework Equations

ΔE_int = Q - W (by the system)
or
ΔE_int = Q + W (on the system)

The Attempt at a Solution

(a)/(b) As the gas moves along the isotherm there is no change in temperature and thus no ΔE_int. My problem comes in (c) when the gas moves to the right. This would mean that positive work is done by the system, which would mean that ΔE_int = Q - W. Why is it that ΔE_int is actually positive in this case?

 

[mjc123]

Any point in region 1 can be reached from the dot by a combination of two moves: a vertical step downwards (decreasing T and P at constant volume) and a move along an isotherm to the final position. (E_int is a state function and therefore path-independent.) What are Q, W and ΔE_int for each of these steps?

 

[L_landau]

Oh I see, for the vertical step downwards T decreases so ΔE_int decreases and along the isotherm ΔE_int=0 so ΔE_int decreases when going to the left!