Moving bar enclosing a changing magnetic field generates a current

[besebenomo]

Homework Statement

A circuit with resistance R, a moving bar of lenght l and mass m has initial velocity along the x-axis = -v and at t=0 the bar is in position x=2l. The circuit lays in a region with depending on the x-coordinate. Find the current flowing in the circuit.

Relevant Equations

Faraday's law

The amplitude of $\vec{B}$ is given by:
$$B(x) = B_{0} - B_{0} \frac{x}{2l}$$ for $0 \leq 0 \leq 2l$

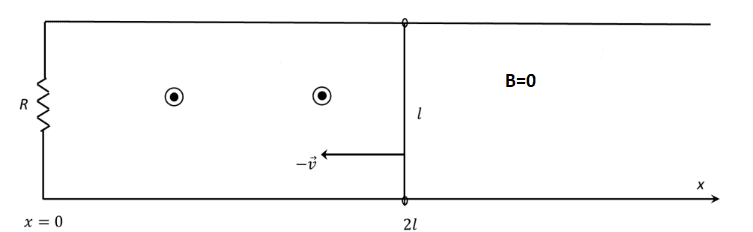
This was my attempts at finding the flux of B:

$$\Phi(B) = (B_{0} - B_{0} \frac{x}{2l})(2l-x(t))l = B_{0}2l^2-2B_{0}x(t)l+ B_{0}\frac{x(t)^2}{2}$$

and the current: $$ i = -\frac{d \Phi(B)}{dt} \frac{1}{R} = -\frac{B_{0} v(t) (2l -x(t))}{R}$$

Is this approach correct?

 

[kuruman]

Is this approach correct?

The current depends on the velocity, so you will have to find that first. I would start with $$I=-\frac{1}{R}\frac{d\Phi}{dt}=-\frac{1}{R}\frac{d(BA)}{dt}$$then use the magnetic force $$\mathbf{F}_M=I\mathbf{L}\times\mathbf{B}$$in Newton's second law. The acceleration is not constant. You will have to solve a differential equation.

The circuit lays in a region with depending on the x-coordinate.

Is something missing from this sentence?

 

[besebenomo]

Is something missing from this sentence?

Yes sorry, I meant B is depending on the x-coordinate.

he acceleration is not constant. You will have to solve a differential equation.

Yes, I know. The problem is that I am not used to solving differential equation when also $x(t)$ is the equation... Is there any way I can rewrite $i$ as a function of only $v(t)$? That way would be so much easier to solve. Maybe I did something wrong when I computed the flux?

 

[kuruman]

You need to write Newton's second law and bring the mass in the equation. What is the net force acting on the bar?

 

[besebenomo]

You need to write Newton's second law and bring the mass in the equation. What is the net force acting on the bar?

The force acting on the bar is the magnetic force, in this case: $$\vec{F}_{mag} = i \vec{l}\times \vec{B} = - \frac{-B_{0} v(t) (2l-x(t)) l}{R} (B_{0} - B_{0} \frac{x(t)}{2l})$$
Then I solve the differential equation, if I didn't make mistakes along the way:
$$m \frac{dv(t)}{dt} = - \frac{-B_{0} v(t) (2l-x(t)) l}{R} (B_{0} - B_{0} \frac{x(t)}{2l}) = - \frac{B_{0}^2 v(t) (2l^2+ \frac{1}{2}x(t)^2)}{R}$$
$$\Longrightarrow \frac{dv(t)}{v(t)} = -\frac{B_{0}^2}{mR}2l^2 dt -\frac{B_{0}^2}{2mR} x(t)^2 dt$$

This is where I get stuck, if there wasn't the second term to the right I would just integrate but I don't really know what to do in this case. That's why I was thinking I did make a mistake in the conceptualization of the problem

 

[kuruman]

A useful method for handling this (some people call it a trick, I call it the chain rule of differentiation) is this
$$a=\frac{dv}{dt}=\frac{dv}{dx}\frac{dx}{dt}=v\frac{dv}{dx}$$ It allows you to separate variables with $v(x)$ on one side and $x$ on the other. Then you integrate. No variable $t$ anywhere.

 

[besebenomo]

A useful method for handling this (some people call it a trick, I call it the chain rule of differentiation) is this
$$a=\frac{dv}{dt}=\frac{dv}{dx}\frac{dx}{dt}=v\frac{dv}{dx}$$ It allows you to separate variables with $v(x)$ on one side and $x$ on the other. Then you integrate. No variable $t$ anywhere.

Thanks a lot you've been really helpful!