Multiple Blocks on incline, friction vs force.

[Semoirethe]

Homework Statement

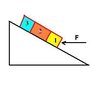
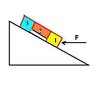
Three blocks are on an incline of Theta(a), block 1 has mass of m1, block 2 has mass of m2, and block 3 has mass of m3. Block 2 is being held(theoretically) above the ground by friction between block 1 and block 3. What is the minimum magnitude of force positioned directly parallel to the x-axis on block 1 required to hold block 2 in the air between the two blocks? The ramp is frictionless and the coefficient of static frictions are us1 and us3 for block 1 and block 3 respectively.

Homework Equations

Fcos(a) - F(n1) - m1gsin(a) = m1aF(n1) - F(n2) - m2gsin(a) = m2aF(n2) - m3gsin(a) = m3aand for the frictionm2gcos(a) - us1F(n1) - us3[F(n2) + m2gsin(a)] = 0

The Attempt at a Solution

I am not sure if my friction equation is correct. I know the friction from the two blocks has to equal m2gcos(a) but I'm not sure if [F(n2) + m2gsin(a)] is correct and if it is, did I place the static friction coefficients backwards? I'm trying to visualize what is happening to that middle block and I feel like the gravity force should be on the first block therefore should use "us1" but that goes against my whole force diagram. So I think I dun goofed. I got an answer but that one point is making me feel that the answer is incorrect. Maybe I'm thinking about friction wrong? The weight force is in the direction of of the normal F(n2) force but since friction only accounts for normal forces then it actually adds to the other normal force?

Hypothetical answer:
F=(m2gcos(a)-us2m2gsin(a))/((us(m2cos(a)+m3cos(a))/(m1+m2+m3)) + (us2(m3cos(a))/(m1+m2+m3))

 

[ehild]

How are the blocks arranged? Is the attached picture correct?


ehild

 

[Semoirethe]

Correct, except block 2 isn't touching the ramp. It's skinnier so it's supposed to be held up by friction between it and the other two blocks.

 

[Fizzicfanatic]

Block #2 is not in contact with the surface of the incline,correct?

My inquiry has already been answered above.Apologies.

 

[ehild]

Is it correct now? Is the x-axis horizontal, or parallel with the slope?

 

[Semoirethe]

Correct. I did the same problem first without the block being on the incline and it equals my answer here with theta = 0. However I do believe I should have taken into account the weight of block 3 pressing on block 2. Aka I messed up the stuff with sin theta >.< aka the whole problem.

It's horizontal.

How exactly do all these mgsin(a)s affect the normal forces?

 

[ehild]

Draw all forces acting on all blocks, and consider the force components separately along the slope and perpendicular to it. There is no friction between the blocks and slope. The frictions act between block 2 and block 1 and block 3 and block2. it is static friction. You know that Fs≤μN. It is not sure that equality holds at both sides of block 2.
All blocks must move with the same acceleration along the slope. How do you get that acceleration?

The acceleration of a single block is determined by the sum of forces acting on it. These forces include the component of gravity along the slope and the normal force from the neighbouring block.

Can you upload pictures?
ehild

 

[Semoirethe]

I found the acceleration to be = [Fcos(a) - (m1+m2+m3)gsin(a))/(m1+m2+m3)]. It's just all the weight "resting" on the middle block that is throwing me off when calculating the correct normal forces for friction. I think I'm having trouble of only looking at block 2 because it feels like everything is getting jumbled.

EDIT: I GOT IT, I'm an idiot. Thanks for your help, it just clicked when I relooked at my equations and actually thought about what they meant.!

 

[ehild]

Splendid!

ehild

 

[Semoirethe]

Thanks for your help. Me and my double and triple counting forces.

 

[digvijay kuma]

digram

How are the blocks arranged? Is the attached picture correct?


ehild

hi , your digram is wrong. the blocks are arranged ina horizontal plane and a side way force is applied ion the block 1 to balance the block 2 in between . so you must try the equation of inertia.

 

[ehild]

Thanks for your help. Me and my double and triple counting forces.

You are welcome. m2gsin(alpha) is exerted by the Earth but the friction is related to the normal force of block 1 to block 2 only.

ehild