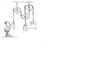Multiple Pulleys and Multiple Weights Problem

[ethancooper]

1. Homework Statement

Solve for T (The force required to keep the pulleys at equilibrium)

See attached image for pulley setup.

2. Homework Equations

W2>W1
N=mg

3. The Attempt at a Solution

Currently I have drawn out all the forces that act on each pulley, and I know there is a way to set up the tensions to solve for T, but since no numerical values are given its a little more complicated.
After applying force diagrams to the hanging weights I got T1=W1g and T3=W2g (with T1 being the tension between Pulley 1 and weight 1, and T3 being the tension between Pulley 2 and weight Which would mean T2=(W2g-W1g)/2, and T2 is the same tension as T, meaning T2 is equivalent to the downward force needed to keep the system at equilibrium. Is this the correct solution?

 

[ethancooper]

for some reason the attachment wouldn't load in original post so here it is again.

 

[haruspex]

That's right, except that if the Ws are weights, not masses, then you don't multiply by g.

 

[ethancooper]

Okay makes sense, thanks for confirming.

 

[Nickie]

I would approach this problem by first identifying the forces acting on each pulley and weight in the system. These forces include the weight of each object (W1 and W2), the tension in the ropes (T1, T2, and T3), and the normal force (N) exerted by the pulleys on the ropes.

Next, I would apply Newton's laws of motion to each pulley and weight to create a system of equations. This would involve setting up equations for the forces in the vertical and horizontal directions and using the fact that the system is at equilibrium, meaning the net force in each direction is equal to zero.

To solve for T, I would use the equations for the vertical forces on each pulley and weight. Since the system is at equilibrium, the sum of all the vertical forces must equal zero. This would result in the equation T1 + T2 + T3 - W1 - W2 = 0. Solving for T, we get T = (W1 + W2)/2, which is the same result as your solution.

In conclusion, your solution is correct. However, I would recommend showing more detailed steps and explanations in your solution, as well as labeling the forces on your force diagrams. This will make your solution clearer and easier to follow for others.