scatterbrainz
- 10
- 1
- TL;DR
- Math - Trig or Physics - Vectors
Hey Everyone,
This is a little project of mine. I'm including a daigram of it - top view -> down. This is part of a larger system.
Consider a fence gate made of poles. In my diagram Point "A" in blue is a non-moving vertical pole. Point "B" red is a pivot point for an arm containing all the points of "C" - purple. Each brown block represents a wood sign that is 5.5 inches wide. Sign "A" rotates around axis "A", signs "B", "C", "D", rotates around their respective axis "C".
The question is, when the arm rotates on axis "B", to a 42.5 deg (+/- 2.5 deg)angle, is the spacing sufficient so that the signs do not overlap each other?
For consideration: when the arm is along the x-plane - the spacing between signs is roughly 5.5 inches, however, it appears to be only 1.5 inches when it is rotated out to 42.5 deg (+/- 2.5 deg). If I remember back to my physic days this screams displacement, but its not just about where the point is when it rotates, its visual space between signs also. Ideas? thoughts ?
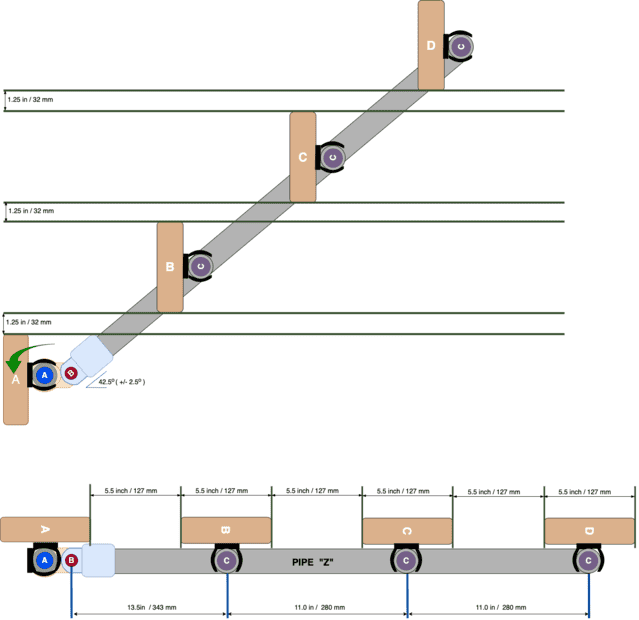
This is a little project of mine. I'm including a daigram of it - top view -> down. This is part of a larger system.
Consider a fence gate made of poles. In my diagram Point "A" in blue is a non-moving vertical pole. Point "B" red is a pivot point for an arm containing all the points of "C" - purple. Each brown block represents a wood sign that is 5.5 inches wide. Sign "A" rotates around axis "A", signs "B", "C", "D", rotates around their respective axis "C".
The question is, when the arm rotates on axis "B", to a 42.5 deg (+/- 2.5 deg)angle, is the spacing sufficient so that the signs do not overlap each other?
For consideration: when the arm is along the x-plane - the spacing between signs is roughly 5.5 inches, however, it appears to be only 1.5 inches when it is rotated out to 42.5 deg (+/- 2.5 deg). If I remember back to my physic days this screams displacement, but its not just about where the point is when it rotates, its visual space between signs also. Ideas? thoughts ?
Last edited by a moderator: