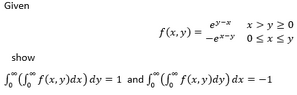Multivariable integration of a piecewise function

[nomadreid]

Homework Statement

Given f(x,y) = exp(y-x) for x>y>=0, and -exp(x-y) for 0<=x<=y, show that the integral from 0 to infinity of (the integral from 0 to infinity of f(x,y) dx)dy=1, and reversing the order of integration, -1.

Relevant Equations

Integrating with respect to one variable, one keeps the other variable as a constant. The integral to infinity is the limit of the integral to an index. Integrating a piecewise function, one integrates each piece.

The problem, neater:

Attempt at a solution:

 

[pasmith]

Write $$\int_0^\infty \left( \int_0^\infty f(x,y)\,dx\right)\,dy = \lim_{Y \to \infty} \int_0^Y \left( \int_0^y f(x,y)\,dx + \lim_{X \to \infty} \int_y^X f(x,y)\,dx \right)\,dy.$$ In the first integral on the right, we have $0 \leq x \leq y$; in the second we have $0 \leq y \leq x$. Take the inner limit first, and simplify the result before doing the outer integral.

 

[nomadreid]

Thanks, pasmith. I will try that.

 

[nomadreid]

Super! I tried it, and not only did it work, but even more important, while doing it I thus understood the reasoning. Thanks again, pasmith!