- #1
Mike400
- 59
- 6
- Homework Statement
- My proof of the theorem : finitely many disjoint discs can be inscribed in a unit square with total area approaching 1
- Relevant Equations
- $$\dfrac{i}{n^2} + \dfrac{b}{n^2} < A + \dfrac{b}{n^2} \tag1$$
$$\text{Area of finite disc packing} = e \dfrac{a- \epsilon}{n^2} + A $$
$$\left[ 1 - A - \dfrac{b}{n^2} \right] (a- \epsilon) + A<a$$
Consider a convex shape ##S## of positive area ##A## inside the unit square. Let ##a≤1## be the supremum of all subsets of the unit square that can be obtained as disjoint union of finitely many scaled and translated copies of ##S##.
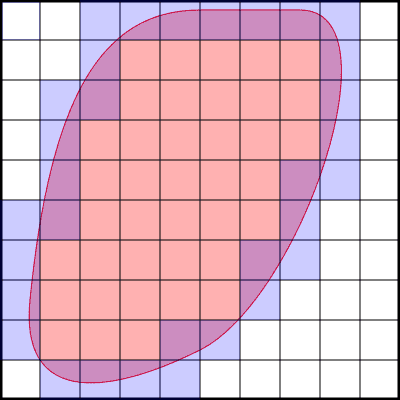
Partition the square into ##n×n## smaller squares (see picture).
There are three types of such small squares: ##e## exterior squares (white in the picture), ##i## interior squares (light red in the image) and ##b## boudary squares (blue/purple). Of course ##e+b+i=n^2##
$$\dfrac{i}{n^2} < A$$
$$\implies\dfrac{i}{n^2} + \dfrac{b}{n^2} < A + \dfrac{b}{n^2} \tag1$$
Picking a finite packing that covers ##\ge a-\epsilon##, for some ##\epsilon##, we can put a scaled-down copy of this packing into each of the ##e## "white" squares and, together with the original shape ##S##, obtain a finite packing of the unit square that covers ##e \dfrac{a- \epsilon}{n^2} + A##. By using this fact and equation ##(1)##
$$a>\text{Area of finite disc packing}
= e \dfrac{a- \epsilon}{n^2} + A$$
$$= \dfrac{e}{n^2} (a- \epsilon) + A
= \left[ 1- \left( \dfrac{i}{n^2} + \dfrac{b}{n^2} \right) \right] (a- \epsilon) + A $$
$$\geq \left[ 1- \left( A + \dfrac{b}{n^2} \right) \right] (a- \epsilon) + A$$
$$=\left[ 1 - A - \dfrac{b}{n^2} \right] (a- \epsilon) + A $$
$$\implies \left[ 1 - A - \dfrac{b}{n^2} \right] (a- \epsilon) + A<a$$
As ##n\to\infty## and ##\epsilon\to 0## the LHS converges to ##a+(1-a)A##. According to a limit theorem, this limit must be ##\le a##. Thus we conclude ##a=1##.
Thus we have shown : finitely many disjoint discs can be inscribed in a unit square with total area approaching 1.
My question : Is my proof of the theorem correct?
Partition the square into ##n×n## smaller squares (see picture).
There are three types of such small squares: ##e## exterior squares (white in the picture), ##i## interior squares (light red in the image) and ##b## boudary squares (blue/purple). Of course ##e+b+i=n^2##
$$\dfrac{i}{n^2} < A$$
$$\implies\dfrac{i}{n^2} + \dfrac{b}{n^2} < A + \dfrac{b}{n^2} \tag1$$
Picking a finite packing that covers ##\ge a-\epsilon##, for some ##\epsilon##, we can put a scaled-down copy of this packing into each of the ##e## "white" squares and, together with the original shape ##S##, obtain a finite packing of the unit square that covers ##e \dfrac{a- \epsilon}{n^2} + A##. By using this fact and equation ##(1)##
$$a>\text{Area of finite disc packing}
= e \dfrac{a- \epsilon}{n^2} + A$$
$$= \dfrac{e}{n^2} (a- \epsilon) + A
= \left[ 1- \left( \dfrac{i}{n^2} + \dfrac{b}{n^2} \right) \right] (a- \epsilon) + A $$
$$\geq \left[ 1- \left( A + \dfrac{b}{n^2} \right) \right] (a- \epsilon) + A$$
$$=\left[ 1 - A - \dfrac{b}{n^2} \right] (a- \epsilon) + A $$
$$\implies \left[ 1 - A - \dfrac{b}{n^2} \right] (a- \epsilon) + A<a$$
As ##n\to\infty## and ##\epsilon\to 0## the LHS converges to ##a+(1-a)A##. According to a limit theorem, this limit must be ##\le a##. Thus we conclude ##a=1##.
Thus we have shown : finitely many disjoint discs can be inscribed in a unit square with total area approaching 1.
My question : Is my proof of the theorem correct?
Last edited by a moderator: