Need help with capacitors and circuits

[Nick L]

Ok, I have 2 homework problems that I don't really know where to even start.
The first one is:
A homemade capacitor is assembled by placing two 15-cm pie tins 20 cm apart and connecting them to opposite terminals of a battery. Calculate the following:
a) the capacitance
b) the charge on each plate
c) the electric field halfway between the plates
d) the work done by the battery to charge the plates

I was able to get part a, but I don't know where to begin for parts b,c, and d.


The second problem uses Kirchhoff's Rules.
Find the current in each of the three resistors of the circuit below:

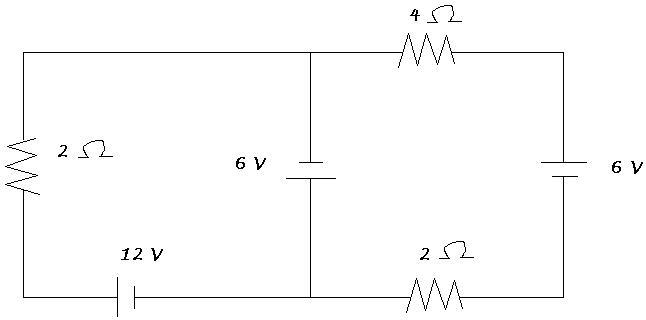
I did not have any idea where to start with this one. I believe it has something to do with loops.

Any help on either of this would really be appreciated.

 

[Mentz114]

Nick, you should show the work you've done with the formulae you've got.
Questions b), c) and d) are all straightforward if you look up the formulae.

The current question needs Kirchoff's rules as you know - so why not look up these rules in a book or in Wiki ...