Need someone with some good CAS

[MigMRF]

Trying to figure out how to model a rocket, and I got some pretty decent flight formulas. The only thing i need is to calculate how fast the masse is expelled. Found an article: (https://www.researchgate.net/publication/253753714_Analysis_of_a_water-propelled_rocket_A_problem_in_honors_physics) which seems to have the solution which is:

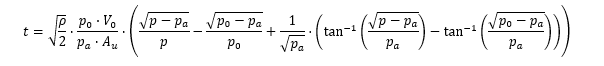
So i tried to solve for p, but my CAS isn't strong enough to solve it. Is there anyone who got an idea of how to solve it.

BTW
If someone manage to solve it, the plan is to but the function inside:

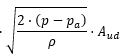
Which gives me the exhaust velocity of the water rocket.

 

[berkeman]

What is CAS?

Google:

 

[TeethWhitener]

CAS = computer algebra system. E.g., Mathematica.

To answer OP, that equation looks pretty transcendental to me. Meaning that there's likely no closed form expression for p. You'd probably be better off tackling it numerically.

 

[kuruman]

The equation posted by OP and printed in the cited AJP article is incorrect. One can see that immediately because (a) the argument of the arctangents is not dimensionless and (b) the time is negative because $p_0>p>p_a$. The correct equation (that still cannot be solved) is$$t=\frac{p_0 V_0}{p_a A_e} \sqrt{\frac{\rho _w}{2}}\left[ \sqrt{ \frac{p_0-p_a}{p_0}}-\sqrt{ \frac{p-p_a}{p}} + \frac{1}{\sqrt{p_a}}\left( \tan ^{-1}\sqrt{\frac{p_0-p_a}{p_a}}-\tan ^{-1}\sqrt{\frac{p-p_a}{p_a}}\right)\right]$$
I got this by solving equation (7) in the reference. It seems that its author dropped the negative sign and coded the radicals incorrectly.