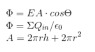Is There Flux Through the Lateral Surface of a Cylinder?
Click For Summary
SUMMARY
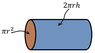
The discussion focuses on calculating the electric flux through the lateral surface of a cylinder. It establishes that the relevant area for flux calculations is the surface area of the ends of the Gaussian surface, given by the formula πR². The enclosed charge is calculated as Q enclosed = 100 * π * (0.1)² * 8.85, resulting in 27.8 pC. It is confirmed that there is no flux through the lateral surface of the cylinder in this specific problem.
PREREQUISITES- Understanding of electric flux and Gauss's Law
- Familiarity with the formula for the surface area of a cylinder
- Knowledge of the concept of Gaussian surfaces in electrostatics
- Basic proficiency in calculus for area calculations
- Study Gauss's Law and its applications in electrostatics
- Learn about calculating electric flux through different geometries
- Explore the implications of enclosed charge on electric fields
- Investigate the role of Gaussian surfaces in simplifying complex electrostatic problems
Students studying electromagnetism, physics educators, and anyone seeking to understand electric flux in cylindrical coordinates.
Similar threads
- · Replies 16 ·
- · Replies 4 ·
- · Replies 7 ·
- · Replies 14 ·
- · Replies 1 ·
- · Replies 10 ·
- · Replies 10 ·