Network, 2 loads, find complex power

[gneill]

Ok, trying again

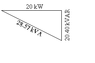
(PL)/(Pf*Vrms) = (Irms)

I_rms = 20000W/(0.7*240V)

I_rms = (119 ∠ 0)A for the 0.7 leading power factor

and

I_rms = (12000VA/240V)

I_rms = (50 ∠ 0)A for the other one


I'll get to the rest of the problem again later

Okay, your apparent current magnitudes look okay, but since there are power factors involved the current angles cannot be zero.

 

[Color_of_Cyan]

So the angles are still cos^-10.7 = 45.5° and cos^-10.9 = 25.8 then?

It would mean

I_rms = (119 ∠ 45.5)A = (83.4 + 84.8j) = for the 0.7 leading power factor and

I_rms = (50 ∠ 25.8)A = (45 + 21.76j) for the 0.9 lagging power factor

then however I_rms = (50 ∠ -25.8)A = (45 - 21.76j) for the 0.9 lagging power factor just for laggingSo I_tot rms = (128.4 + 63j)A = (143 ∠ 114)AThen the series Z is still (0.05 + 0.2j)Ω = (0.206 ∠ 76)Ω

So V_drop = (0.206 ∠ 76)Ω * (143 ∠ 114)A

V_drop = (29.45 ∠ 190)V = (-29 - 5.1j)VV_tot = (211 - 5.1j)V = ( 211 ∠ -1.38)VThen for the apparent power with this I got

(143A)*(211V) = 30kVA now

 

[gneill]

So the angles are still cos^-10.7 = 45.5° and cos^-10.9 = 25.8 then?

It would mean

I_rms = (119 ∠ 45.5)A = (83.4 + 84.8j) = for the 0.7 leading power factor and

I_rms = (50 ∠ 25.8)A = (45 + 21.76j) for the 0.9 lagging power factor

then however I_rms = (50 ∠ -25.8)A = (45 - 21.76j) for the 0.9 lagging power factor just for lagging


So I_tot rms = (128.4 + 63j)A = (143 ∠ 114)A

With real and imaginary terms of 128 and 63 the resulting angle should lie in the 1st quadrant (so, less than 90°). Check your angle calculation. The calculations that follow will depend upon this.

 

[Color_of_Cyan]

I got confused and converted just that the other way (polar to rectangular for that instead of rectangular to polar instead), it seems.

Starting it over then:

I_rms = (119 ∠ 45.5)A = (83.4 + 84.8j) = for the 0.7 leading power factor and

I_rms = (50 ∠ 25.8)A = (45 + 21.76j) for the 0.9 lagging power factor

then I_rms = (50 ∠ -25.8)A = (45 - 21.76j) for the 0.9 lagging power factor just for laggingNow the correction I_totrms = (128.4 + 63j)A = (143 ∠ 26.1)ASeries Z is still (0.05 + 0.2j)Ω = (0.206 ∠ 76)Ω

V_drop = (0.206 ∠ 76)Ω * (143 ∠ 26.1)A

V_drop = (29.45 ∠ 102)V = (-6.12 + 28.8)VV_tot = (233 + 28.8j)V = (234 ∠ 7.04)VApparent power = (143A)*(243V) = 34.7kVA

 

[gneill]

I got confused and converted just that the other way (polar to rectangular for that instead of rectangular to polar instead), it seems.

Starting it over then:

I_rms = (119 ∠ 45.5)A = (83.4 + 84.8j) = for the 0.7 leading power factor and

I_rms = (50 ∠ 25.8)A = (45 + 21.76j) for the 0.9 lagging power factor

then I_rms = (50 ∠ -25.8)A = (45 - 21.76j) for the 0.9 lagging power factor just for lagging


Now the correction I_totrms = (128.4 + 63j)A = (143 ∠ 26.1)A


Series Z is still (0.05 + 0.2j)Ω = (0.206 ∠ 76)Ω

V_drop = (0.206 ∠ 76)Ω * (143 ∠ 26.1)A

V_drop = (29.45 ∠ 102)V = (-6.12 + 28.8)V


V_tot = (233 + 28.8j)V = (234 ∠ 7.04)V

240 - 6.12 = 233.88 which rounds to 234.

Be careful with your digits and rounding through intermediate steps. It's better to hang onto several more digits and do no rounding at all through intermediate values. The more steps a problem has where each next step depends upon values from previous steps, the greater the danger of rounding and truncation errors creeping into the significant figures.

Apparent power = (143A)*(243V) = 34.7kVA

Okay. So it looks like you've got a correct approach to the problem. Just work out the accuracy issue with rounding/truncation on intermediate steps (For comparison purposes, with no rounding or truncation through the process I find that the apparent power, to three decimals, turns out to be 33.697 kVA which would round to 34 kVA for presentation).

 

[Color_of_Cyan]

Well, thanks for the heads up. Doing that again I got this:

I_rms = (119 ∠ 45.5)A = (83.408 + 84.87j) = for the 0.7 leading power factor and

I_rms = (50 ∠ 25.8)A = (45.01 + 21.761j) for the 0.9 lagging power factor

then Irms = (50 ∠ -25.8)A = (45.01 - 21.761j) for the 0.9 lagging power factor just for lagging


I_totrms = (128.4 + 63j)A = (143.02 ∠ 26.135)A


Series Z is still (0.05 + 0.2j)Ω = (0.2061 ∠ 75.963)Ω

V_drop = (0.2061 ∠ 75.963)Ω * (143.02 ∠ 26.135)A

V_drop = (29.476 ∠ 102.098)V = (-6.177 + 28.821j)V


V_tot = (233.823 + 28.821j)V = (235.59 ∠ 7.0268)V


Apparent power = (143.02A)*(235.59V) = 33.694kVA

I know it makes a difference, although still not exactly what you have.


Now then

The total impedance is Z = V/I

Z_tot = (235.59 ∠ 7.0268)V/(143.02 ∠ 26.135)A

Z_tot = (1.647 ∠ 33.161)Ω = (1.3787 + 0.9j)Ω

Would the power factor of the source be cos(total impedance angle) ?

ie cos(33.161) = 0.837 ?

Would Vs(t) just be V_tot in max value form? I should probably also say that on the paper with this problem there is no "Vs(t)" (but just Vs) on the diagram even though it asks to find Vs(t). It's supposed to be that way though right?

ie Vs(t) = (235.59 ∠ 7.0268)V*√2 = (333.17 ∠ 7.0268)V max ?

Is the complex power also 33.697kVA? How do you understand the difference between complex / apparent power better?

 

[gneill]

Well, thanks for the heads up. Doing that again I got this:



I know it makes a difference, although still not exactly what you have.


Now then

The total impedance is Z = V/I

Z_tot = (235.59 ∠ 7.0268)V/(143.02 ∠ 26.135)A

Z_tot = (1.647 ∠ 33.161)Ω = (1.3787 + 0.9j)Ω

Careful. When dividing complex numbers in polar form you subtract the angle of the denominator from the angle of the numerator...

Would the power factor of the source be cos(total impedance angle) ?

ie cos(33.161) = 0.837 ?

I suppose that would be it. To me it's a bit of an odd way to describe a source (as having a power factor rather than phase angle). Get your impedance angle correct first!

Would Vs(t) just be V_tot in max value form?

What's V_tot ?

By "max value form" I presume you mean the time-domain peak value expression for supply voltage? If so then you'd find the peak value from the RMS value that you've calculated, determine the phase angle from the "power factor" above, then write it out:

$V(t) = V_m cos(ω t + \phi)$

Is the complex power also 33.697kVA? How do you understand the difference?

33.697kVA is the apparent power. It's the magnitude of the complex power phasor. There's a real power and reactive power (imaginary) component. Look up "power triangle".

 

[Color_of_Cyan]

Okay, my mistake again

Z_tot = (235.59 ∠ 7.0268)V/(143.02 ∠ 26.135)A

Z_tot = 1.647 ∠ -19.108

then the power factor (of the source) would be

cos(-19.108) = 0.94

To me it's a bit of an odd way to describe a source (as having a power factor rather than phase angle). Get your impedance angle correct first!

But the angle for calculating any power factor is always from the impedance angle though right? The impedance angle always means it's the phase?

I presume you mean the time-domain peak value expression for supply voltage?

Thanks again.

So for that equation

Vm = (235.59 ∠ 7.0268)V*√2

Vm = (333.17 ∠ 7.0268)V max

ω = 0.0166

Vs(t) = 333.17*cos(0.0166t - 19.108°)

This is what was really meant by Vs(t)? It seems more like a fixed equation than any value, but I understand, it just seems strange and there are lots of formulas with time domain and I couldn't figure out which one was which. It's fine though I guess.

33.697kVA is the apparent power. It's the magnitude of the complex power phasor. There's a real power and reactive power (imaginary) component. Look up "power triangle".

For fun now the real power of the source is 33.697*cos(-19.108) = 31.84W

and the reactive power = 33.697 * sin(-19.108) = -11.03 VARS?

 

[gneill]

Okay, my mistake again

Z_tot = (235.59 ∠ 7.0268)V/(143.02 ∠ 26.135)A

Z_tot = 1.647 ∠ -19.108

then the power factor (of the source) would be

cos(-19.108) = 0.94

That looks okay.

But the angle for calculating any power factor is always from the impedance angle though right? The impedance angle always means it's the phase?

The load is not the source. The question asked for the power factor of the source, which I find a bit odd. Interpreting it as simply the cosine of the phase angle attributed to the source seems like the best interpretation to me.

Thanks again.

So for that equation

Vm = (235.59 ∠ 7.0268)V*√2

Vm = (333.17 ∠ 7.0268)V max

ω = 0.0166

Vs(t) = 333.17*cos(0.0166t - 19.108°)

Yup. Looks okay, if you really need the expression for the peak voltage.

This is what was really meant by Vs(t)? It seems more like a fixed equation than any value, but I understand, it just seems strange and there are lots of formulas with time domain and I couldn't figure out which one was which. It's fine though I guess.

For sinusoidal voltage supplies the peak and RMS values are always related by a factor of √2. The phasor representation simply omits the ωt information of the time domain formula, since ωt is a common component of all the phasors (current, voltage) throughout the circuit.

In power systems RMS values are almost always intended or implied. Unless otherwise specifically instructed or indicated, always assume that RMS values are given. For example, a typical North American domestic 110 V power outlet means 110V RMS.

For fun now the real power of the source is 33.697*cos(-19.108) = 31.84W

and the reactive power = 33.697 * sin(-19.108) = -11.03 VARS?

Sure. Once again, I suggest that you investigate the Power Triangle to relate these values graphically.

 

[NascentOxygen]

ω = 1/f = 0.0166

$ω = 2 \pi f$[/color]

 

[Color_of_Cyan]

Ok, thanks for catching that. I thought there was something different between period and ω but couldn't remember.

ω = 376.9